题目内容
7.如果点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|,那么|AB|=|a-b|,根据这个公式解答下列问题:(1)数轴上表示2和5两点之间的距离是3,数轴上表示-2和-5两点之间的距离是3;数轴上表示1和-$\sqrt{3}$两点之间的距离是1+$\sqrt{3}$.
(2)若数轴上A、B两点分别表示实数x和-$\sqrt{2}$,且|AB|=3,求x的值;
(3)若数轴上的三点P、A、B分别表示实数x,-$\sqrt{2}$和$\sqrt{3}$,求当代数式|x+$\sqrt{2}$|+|x-$\sqrt{3}$|取最小值时x的取值范围.
分析 (1)直接利用|AB|=|a-b|,分别求出答案;
(2)根据数轴上两点间的距离公式可知AB=|x+$\sqrt{2}$|=3,再根据绝对值的性质求出x的值即可;
(3)由线段的性质,两点之间,线段最短,可知当-$\sqrt{2}$≤x≤$\sqrt{3}$时,|x+$\sqrt{2}$|+|x-$\sqrt{3}$|有最小值.
解答 解:(1)数轴上表示2和5两点之间的距离是:|2-5|=3,
数轴上表示-2和-5两点之间的距离是:|-2-(-5)|=3,
数轴上表示1和-$\sqrt{3}$两点之间的距离是:|1-(-$\sqrt{3}$)|=1+$\sqrt{3}$;
故答案为:3,3,1+$\sqrt{3}$;
(2)∵数轴上A、B两点分别表示实数x和-$\sqrt{2}$,且|AB|=3,
∴|x+$\sqrt{2}$|=3,
则x+$\sqrt{2}$=±3,
解得:x=-$\sqrt{2}$±3;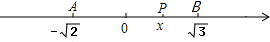
(3)如图,代数式|x+$\sqrt{2}$|取最小值时,即P到A、B的距离之和最小,
此时,P在A、B之间,
则-$\sqrt{2}$≤x≤$\sqrt{3}$.
点评 本题考查了实数与数轴、绝对值,解答此题的关键是要明确:|x-a|既可以理解为x与a的差的绝对值,也可理解为x与a两数在数轴上所对应的两点之间的距离.

练习册系列答案
相关题目
 一个装有进水管和出水管的容器,从某时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进、出水管.在打开进水管到关停进、出水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示
一个装有进水管和出水管的容器,从某时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进、出水管.在打开进水管到关停进、出水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示



 元旦期间,胡老师开车从扬州到相距150千米的老家探亲,如果油箱里剩余油量 y(升)与行驶里程 x(千米)之间是一次函数关系,其图象如图所示,那么胡老师到达老家时,油箱里剩余油量是20升.
元旦期间,胡老师开车从扬州到相距150千米的老家探亲,如果油箱里剩余油量 y(升)与行驶里程 x(千米)之间是一次函数关系,其图象如图所示,那么胡老师到达老家时,油箱里剩余油量是20升.