题目内容
已知一个多边形的内角和等于它的外角和的3倍,那么它的边数是( )
A.5 B.6 C.7 D.8
D【考点】多边形内角与外角.
【分析】根据多边形的内角和等于它的外角和的3倍可求得多边形的内角和,然后利用多边形的内角和公式计算即可.
【解答】解:∵多边形的内角和等于它的外角和的3倍,
∴多边形的内角和=360°×3.
设多边形的边数为n,根据题意得:(n﹣2)×180°=360°×3.
解得n=8.
故选:D.
【点评】本题主要考查的是多边形的内角和与外角和,掌握多边形的内角和公式是解题的关键.

练习册系列答案
相关题目
 ﹣
﹣ )2
)2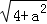 ,
,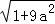 ,
,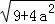 (a为正整数)三角形的面积.
(a为正整数)三角形的面积.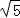 、
、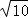 、
、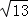 三角形的面积.
三角形的面积.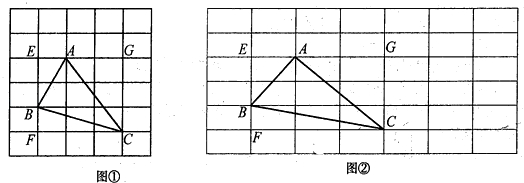
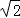 ,
,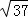 ,5三角形的面积.
,5三角形的面积. 别为2
别为2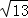 ,
, ,3
,3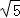 三角形的
三角形的
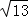 ,
,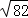 ,3
,3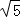 的三角形的面积为__________.
的三角形的面积为__________.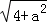 ,
, ,
,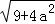 (a为正整数)三角形的面积.
(a为正整数)三角形的面积.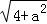 ,
,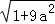 ,
,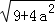 (a为正整数)的三角形的面积是__________.
(a为正整数)的三角形的面积是__________.