Question

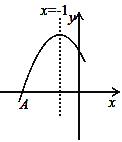
【题目】已知二次函数y＝x2+bx+c+1的图象与x轴交于点A（x1，0）、B（x2，0），且x1＜x2，与y轴的负半轴交于点C．

（1）当b＝1时，求c的取值范围；

（2）如果以AB为直径的半圆恰好过点C，求c的值；

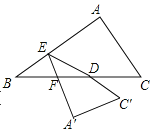
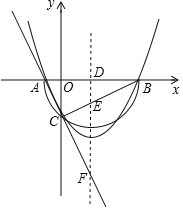
（3）在（2）的条件下，如果二次函数的对称轴l与x轴、直线BC、直线AC的延长线分别交于点D、E、F，且满足DE＝2EF，求二次函数的表达式．

Answer 1

【答案】（1）c＜﹣1；（2）c的值为﹣2；（3）y＝ ．

【解析】

（1）有两个交点则△＝0，从而可解；

（2）直径所对的圆周角为直角，再利用斜边中线等于斜边一半可解；

（3）由平行得相似，从而列比例式可解.

（1）已知二次函数y＝x2+bx+c+1的图象与x轴交于点A（x1，0）、B（x2，0），当b＝1时，

令x2+bx+c+1＝0，则△＝b2﹣4（c+1）＝1﹣4c﹣4＞0

∴，

考虑点C在负半轴，则c+1＜0，

∴c＜﹣1．

当b＝1时，求c的取值范围是c＜﹣1．

（2）∵C（0，c+1），

令x2+bx+c+1＝0，解得点A（，0），点B（，0），

如果以AB为直径的半圆恰好过点C，则由直径所对的圆周角为直角，得∠ACB＝90°，二次函数的对称轴l与x轴交于点D，则D（，0），

∴CD＝，即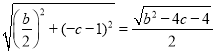，化简得c2+3c+2＝0，

∴c＝﹣2或c＝﹣1（舍）．

答：c的值为﹣2．

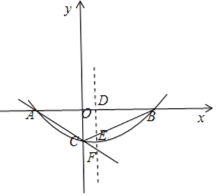
（3）设EF＝k，DE＝2K，

∵DE∥OC，

∴△DEB～△OCB，

∴，

∴，

∵OC∥DF，

∴△AOC～△ADF

∴，

∴，

∵AD＝BD，

∴

又∵x1x2＝﹣1，

∴，

∴

∴二次函数的表达式为：．