��Ŀ����
��ͼ1����ƽ��ֱ������ϵ�У�������y=ax2+bx+3��x����A��﹣1��0����B��5��0�����㣬��y���ڵ�C����D���߶�OB��һ���㣬����CD�����߶�CD�Ƶ�D˳ʱ����ת90��õ��߶�DE������E��ֱ��l��x����H������C��CF��l��F��
��1���������߽���ʽ��
��2����ͼ2������Fǡ������������ʱ�����߶�OD�ij���
��3���ڣ�2���������£�
������DF����tan��FDE��ֵ��
����̽����ֱ��l�ϣ��Ƿ���ڵ�G��ʹ��EDG=45�㣿�����ڣ���ֱ��д����G�����ꣻ�������ڣ���˵�����ɣ�
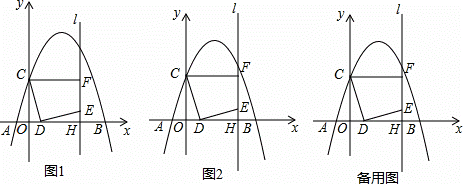
�⣺��1����ͼ1����������y=ax2+bx+3��x����A��﹣1��0����B��5��0�����㣬
�� ��
��
��� ��
��
�������߽���ʽΪy=﹣ x2+
x2+ x+3��
x+3��
��2����ͼ2���ߵ�Fǡ�����������ϣ�C��0��3����
��F��������Ϊ3��
��y=3����y=﹣ x2+
x2+ x+3�ã�3=﹣
x+3�ã�3=﹣ x2+
x2+ x+3��
x+3��
���x=0��x=4��
��F��4��3����
��OH=4��
�ߡ�CDE=90�㣬
���ODC+��EDH=90�㣬
���OCD=��EDH��
�ڡ�OCD�͡�HDE�У�
 ��
��
���OCD�ա�HDE��AAS����
��DH=OC=3��
��OD=4﹣3=1��
��3������ͼ3������CE��
�ߡ�OCD�ա�HDE��
��HE=OD=1��
��BF=OC=3��
��EF=3﹣1=2��
�ߡ�CDE=��CFE=90�㣬
��C��D��E��F�ĵ㹲Բ��
���ECF=��EDF��
��RT��CEF����CF=OH=4��
��tan��ECF= =
= =
= ��
��
��tan��FDE= ��
��
����ͼ4������CE��
��CD=DE����CDE=90�㣬
���CED=45�㣬
��D����DG1��CE����ֱ��l��G1����D����DG2��CE����ֱ��l��G2�����EDG1=45�㣬��EDG2=45��
��EH=1��OH=4��
��E��4��1����
��C��0��3����
��ֱ��CE�Ľ���ʽΪy=﹣ x+3��
x+3��
��ֱ��DG1�Ľ���ʽΪy=﹣ x+m��
x+m��
��D��1��0����
��0=﹣ ��1+m�����m=
��1+m�����m= ��
��
��ֱ��DG1�Ľ���ʽΪy=﹣ x+
x+ ��
��
��x=4ʱ��y=﹣ +
+ =﹣
=﹣ ��
��
��G1��4��﹣ ����
����
��ֱ��DG2�Ľ���ʽΪy=2x+n��
��D��1��0����
��0=2��1+n�����n=﹣2��
��ֱ��DG2�Ľ���ʽΪy=2x﹣2��
��x=4ʱ��y=2��4﹣2=6��
��G2��4��6����
���ϣ���ֱ��l�ϣ��Ƿ���ڵ�G��ʹ��EDG=45�㣬��G������Ϊ��4��﹣ ����4��6����
����4��6����





 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�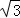 ����tan��DEM=1��
����tan��DEM=1�� ��1.41��
��1.41��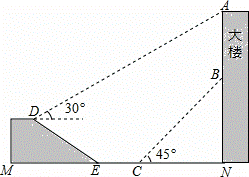

 B��
B�� C��
C�� D��
D��
 ���������Ľ⼯�������ϱ�ʾ������
���������Ľ⼯�������ϱ�ʾ������