题目内容
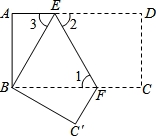
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)折叠后,DC的对应线段是__________,CF的对应线段是__________;
(2)若AB=8,DE=10,求CF的长度.
【考点】翻折变换(折叠问题).
【分析】(1)根据翻折后的对应点确定出对应线段即可;
(2)在Rt△ABE中由勾股定理可求得AE=6,从而得到AD=16,然后证明BE=BF=10,从而可求得FC=16﹣10=6.
【解答】解:(1)∵点D与点B重合,点C落在点C′的位置上,
∴DC的对应线段是BC′,CF的对应线段是FC′.
故答案为:BC′;FC′.
(2)由翻折的性质可知:DE=BE=10,∠2=∠BEF.
∵AD∥BC,
∴∠2=∠1.
∴∠1=∠BEF.
∴BE=BF=10.
在Rt△A BE中,由勾股定理得:AE=
BE中,由勾股定理得:AE=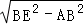 =
=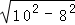 =6,
=6,
∴AD=AE+ED=6+10=16.
∴CF=CB﹣BF=16﹣10=6.
【点评】本题主要考查的是翻折的性质、勾股定理的应用,证得BE=BF=10是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 B.
B. C.
C. D.
D.
 上且CE=CA,试求∠DAE的度数;
上且CE=CA,试求∠DAE的度数;