题目内容
9．
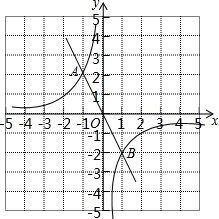如图，正比例函数y1=kx和反比例函数y2=$\frac{{k}^{2}}{x}$的图象交于A（-1，2）、（1，-2）两点，若y1＜y2，则x的取值范围是-1＜x＜0或x＞1．
分析 根据A、B的横坐标，结合图象即可得出当y1＜y2时x的取值范围．
解答 解：∵正比例函数y1=kx和反比例函数y2=$\frac{{k}^{2}}{x}$的图象交于A（-1，2）、（1，-2）两点，y1＜y2，
∴∴此时x的取值范围是-1＜x＜0或x＞1，
故答案为：-1＜x＜0或x＞1．
点评 本题考查了一次函数与反比例函数的交点问题，主要考查学生的理解能力和观察图形的能力，题目具有一定的代表性，是一道比较好的题目，用了数形结合思想．
练习册系列答案
全能测控期末小状元系列答案
智趣暑假温故知新系列答案
相关题目
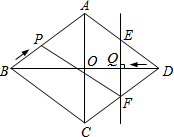已知：如图，菱形ABCD中，对角线AC，BD相交于点O，且AC=12cm，BD=16cm．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，直线EF从点D出发，沿DB方向匀速运动，速度为1cm/s，EF⊥BD，且与AD，BD，CD分别交于点E，Q，F；当直线EF停止运动时，点P也停止运动．连接PF，设运动时间为t（s）（0＜t＜8）．解答下列问题：
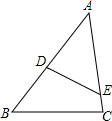如图，在△ABC中，点D、E分别在AB、AC上，∠ADE=∠C，如果AE=4cm，△ADE的面积是4cm2，四边形BCED的面积是5cm2，那么AB的长是6cm．
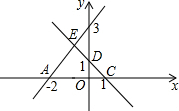如图，直线AB分别与x轴、y轴交于点A（-2，0），B（0，3）．直线CD分别与x轴、y轴交于点C（1，0），D（0，1），与直线AB交于点E．求点E的坐标．
18．下列各式中，互为相反数的两个数是（ ）
| A． | -5与$\frac{1}{5}$ | B． | |-$\frac{1}{2}$|与$\frac{1}{2}$ | C． | -2$\frac{1}{2}$与-0.4 | D． | -（-5）与-5 |