题目内容
解下列方程
(1)
-
=-2;
(2)
-
=1.
(1)
| 3 |
| x-2 |
| x |
| 2-x |
(2)
| x+1 |
| x-1 |
| 4 |
| x2-1 |
考点:解分式方程
专题:计算题,转化思想
分析:两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答:(1)解:两边同乘x-2,得:3+x=-2(x-2),
去括号得:3+x=-2x+4,
移项合并得:3x=1,
解得:x=
,
经检验,x=
是原方程的解;
(2)两边同乘(x-1)(x+1),得:(x+1)2-4=x2-1,
去括号得:x2+2x+1-4=x2-1,
移项合并得:2x=2,
解得:x=1,
经检验,x=1是原方程的增根,
则原方程无解.
去括号得:3+x=-2x+4,
移项合并得:3x=1,
解得:x=
| 1 |
| 3 |
经检验,x=
| 1 |
| 3 |
(2)两边同乘(x-1)(x+1),得:(x+1)2-4=x2-1,
去括号得:x2+2x+1-4=x2-1,
移项合并得:2x=2,
解得:x=1,
经检验,x=1是原方程的增根,
则原方程无解.
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
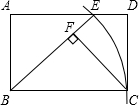 如图,在矩形ABCD中,以顶点B为圆心、边BC长为半径作弧,交AD边于点E,连结BE,过C点作CF⊥BE于F.
如图,在矩形ABCD中,以顶点B为圆心、边BC长为半径作弧,交AD边于点E,连结BE,过C点作CF⊥BE于F.