题目内容
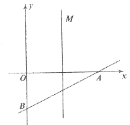
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交
轴分别交![]() 、
、![]() 两点,点
两点,点![]() 关于原点
关于原点![]() 的对称点是点
的对称点是点![]() .动点
.动点![]() 从
从![]() 出发以每秒1个单位的速度运动到点
出发以每秒1个单位的速度运动到点![]() ,点
,点![]() 在线段
在线段![]() 上满足
上满足![]() ,过
,过![]() 点作
点作![]() 于点
于点![]() ,点
,点![]() 关于点
关于点![]() 的对称点为点
的对称点为点![]() ,以
,以![]() 为直径作
为直径作![]() ,设点
,设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
(1)当点![]() 在段
在段![]() 上运动,
上运动,![]() ______时,
______时,![]() 与
与![]() 的相似比为
的相似比为![]() ;
;
(2)当![]() 与
与![]() 轴相切时,求
轴相切时,求![]() 的值;
的值;
(3)若直线![]() 与
与![]() 交于点
交于点![]() ,是否存在使
,是否存在使![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先求直线与坐标轴的交点坐标,再证△AEF∽△EDO∽△ABO,由△AEF与△EDO的相似比为![]() ,即可求得t的值;
,即可求得t的值;
(2)由⊙M与y轴相切可知:DG⊥y轴,分两种情况:0≤t≤3或3<t≤6,用含![]() 的表示AE,OE,OD,BD再利用三角形的相似与点
的表示AE,OE,OD,BD再利用三角形的相似与点![]() 关于点
关于点![]() 的对称点为点
的对称点为点![]() 可得答案.
可得答案.
(3)分三种情况:0≤t≤![]() 或
或 ![]() <t≤3或3<t≤6,分别建立方程求解即可.
<t≤3或3<t≤6,分别建立方程求解即可.
(1)由![]() ,可得:
,可得:![]()
∴OA=3,OB=6,![]() ,
,![]() ,
,
∴tan∠BAO=![]()
∵tan∠DEO=2
∴∠BAO=∠DEO
∵EF⊥AB ∴∠AFE=∠DOE=90°
∴△AEF∽△EDO∽△ABO
![]() ,即:
,即:![]() ,
,
∴![]() ;
;
∵△AEF与△EDO的相似比为![]() ,
,
∴ ![]() ,即
,即![]()
∴![]() , 解得:
, 解得:![]() ;
;
故答案为:![]() ;
;
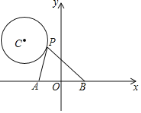
(2)![]() 与
与![]() 轴相切,则
轴相切,则![]() 轴
轴
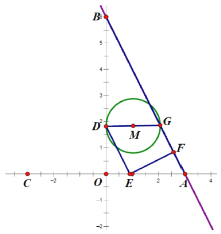
当点![]() 在
在![]() 线段上时,即
线段上时,即![]() 时,如图,此时
时,如图,此时![]() ,
,![]() ,则由
,则由![]() 可知,
可知,![]() ,则
,则![]() ;又易证
;又易证![]() ,故可得
,故可得![]() ,又点
,又点![]() 是点
是点![]() 关于点
关于点![]() 的对称点,所以
的对称点,所以![]() ,故
,故![]() ;又
;又![]() 轴,则
轴,则![]() ,即
,即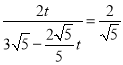 ,解得
,解得![]() ;
;

当点![]() 在
在![]() 线段上时,即
线段上时,即![]() 时,如图,此时
时,如图,此时![]() ,
,![]() ,则
,则![]() ,故此时
,故此时![]() ,而
,而![]() 保持不变;又
保持不变;又![]() 轴,则
轴,则![]() ,即
,即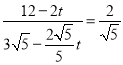 ,解得
,解得![]() .
.
综上,当![]() 或
或![]() 时,
时,![]() 与
与![]() 轴相切.
轴相切.
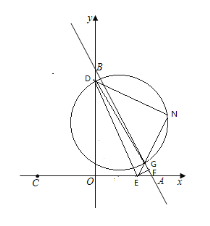
(3)当![]() 时, ∵点A关于点F的对称点为点G,EF⊥AB
时, ∵点A关于点F的对称点为点G,EF⊥AB
∴EG=EA=t ∵∠OEG=∠OAB+∠EGA=2∠OAB,∠OED=∠OAB
∴∠DEG=∠DEG ∵DG为直径 ∴∠DNG=∠DOE=90°,又DE=DE
∴△DEN≌△DEO(AAS)
∴![]()
由NG=NA得:![]() , 解得:
, 解得:![]()
同理,当![]() 时,因为点
时,因为点![]() 与点
与点![]() 关于点
关于点![]() 对称,所以易得
对称,所以易得![]() ,又
,又![]() 为
为![]() 的直径,所以
的直径,所以![]() .
.
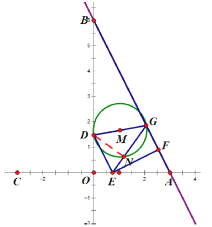
如图,此时易证![]() ,所以
,所以![]() ,故有
,故有![]() ,解得
,解得![]() .
.
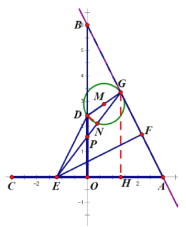
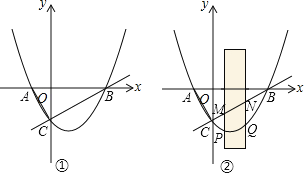
当点![]() 在
在![]() 线段上时,即
线段上时,即![]() 时,此时大致图形如图所示,设
时,此时大致图形如图所示,设![]() 与
与![]() 轴的交点为点
轴的交点为点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,则由面积关系可得
,则由面积关系可得![]() ,易得
,易得![]() ,即
,即![]() ,又
,又![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,又
,又![]() ,
,
所以![]() ,
,
又![]() ,即
,即![]() ,
,
解得:![]()
综上,当![]() 或
或![]() 或
或![]() 时,
时,![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案