��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У���������������κ���![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() �͵�
�͵�![]() ��
��
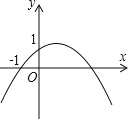
��1����![]() ʱ�����������Ľ���ʽ��
ʱ�����������Ľ���ʽ��
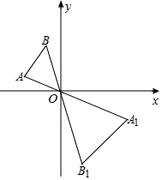
��2����֪����ԭ��O������ֱ��AB��CD�ֱ���˫����![]() ����A��B��C��D����ôAB��CD����ƽ�֣������ı���ACBD��ƽ���ı����ʣ�ƽ���ı���ACBD�ܷ��Ϊ���Σ��ܷ��Ϊ�����Σ����ܣ���˵���߶�AB��CD��λ�ù�ϵ�������ܣ���˵�����ɣ�
����A��B��C��D����ôAB��CD����ƽ�֣������ı���ACBD��ƽ���ı����ʣ�ƽ���ı���ACBD�ܷ��Ϊ���Σ��ܷ��Ϊ�����Σ����ܣ���˵���߶�AB��CD��λ�ù�ϵ�������ܣ���˵�����ɣ�
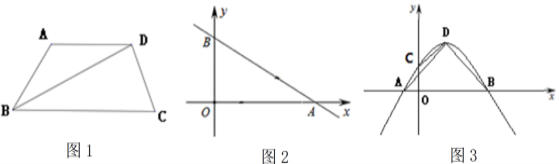
��3������κ�����ͼ��Ķ���ΪQ������ABQ����ABΪб�ߵ�ֱ��������ʱ����k��ֵ��
���𰸡���1��![]() ����2���ܳ�Ϊ���Σ����ܳ�Ϊ�����Σ��߶�AB��CD����ƽ������ȣ���3��k��ֵΪ
����2���ܳ�Ϊ���Σ����ܳ�Ϊ�����Σ��߶�AB��CD����ƽ������ȣ���3��k��ֵΪ![]() ��
��![]() ��
��
��������
��1��ֱ�Ӱѵ�A��1��k�����뷴���������Ľ���ʽ���ɣ��ٰ�k��2���뼴�ɣ�
��2������A��C�������ӽ�����ϵ���Dz��������������ϣ���AB��CD����ֱ���ʿɵó����ۣ�
��3���Ȱ�k������֪������ʾ��Q������꣬����A��B����ԭ��O���ĶԳƿ�֪��OQ��OA��OBʱ����ABQ����ABΪб�ߵ�ֱ�������Σ���OQ2��OA2�����ɵó�����k��һԪ���η��̣����k��ֵ���ɣ�
��1��![]() ������������ͼ�����
������������ͼ�����![]() ��
��
![]() �����������Ľ���ʽ��
�����������Ľ���ʽ��![]() ��
��
��![]() ʱ�������������Ľ���ʽ��
ʱ�������������Ľ���ʽ��![]() ��
��
��2���ܳ�Ϊ���Σ����ܳ�Ϊ�����Σ��߶�AB��CD����ƽ������ȣ�
��AB��CD����ֱ��![]() ��
��![]() �Գ�ʱ��AB��CD����ƽ������ȣ�
�Գ�ʱ��AB��CD����ƽ������ȣ�
![]() �ı���ACBD�ܳ�Ϊ���Σ�
�ı���ACBD�ܳ�Ϊ���Σ�
![]() ��A��B��C��D�������ӽ������ᵫ�Dz��������������ϣ�
��A��B��C��D�������ӽ������ᵫ�Dz��������������ϣ�
![]() AB��CD����ֱ��
AB��CD����ֱ��
![]() �ı���ACBD���ܳ�Ϊ�����Σ�
�ı���ACBD���ܳ�Ϊ�����Σ�
��3��![]() ���κ����Ķ���Q��������
���κ����Ķ���Q��������![]() ��A��B����ԭ��O���ĶԳƣ�
��A��B����ԭ��O���ĶԳƣ�
![]() ��
��![]() ʱ��
ʱ��![]() ����ABΪб�ߵ�ֱ�������Σ�
����ABΪб�ߵ�ֱ�������Σ�
��![]() ����
���� ��
��
���![]() ��
��![]() ��
��
![]() ��
��![]() ����ABΪб�ߵ�ֱ��������ʱ��k��ֵΪ
����ABΪб�ߵ�ֱ��������ʱ��k��ֵΪ![]() ��
��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�