题目内容
有理数a,b满足ab=1,设M=
+
;N=
+
,求证:M=N.
| 1 |
| 1+a |
| 1 |
| 1+b |
| a |
| 1+a |
| b |
| 1+b |
考点:分式的加减法
专题:证明题
分析:把M=
+
和N=
+
通分,化简M,N,再证明M=N即可.
| 1 |
| 1+a |
| 1 |
| 1+b |
| a |
| 1+a |
| b |
| 1+b |
解答:解:∵ab=1,
∴M=
+
=
+
=
=
=1;
N=
+
=
+
=
=
=1,
∴M=N.
∴M=
| 1 |
| 1+a |
| 1 |
| 1+b |
=
| 1+b |
| (1+a)(1+b) |
| 1+a |
| (1+a)(1+b) |
=
| 2+a+b |
| (1+a)(1+b) |
=
| 2+a+b |
| 1+a+b+ab |
=1;
N=
| a |
| 1+a |
| b |
| 1+b |
=
| a(1+b) |
| (1+a)(1+b) |
| b(1+a) |
| (1+a)(1+b) |
=
| a+ab+b+ab |
| (1+a)(1+b) |
=
| 2+a+b |
| 1+a+b+ab |
=1,
∴M=N.
点评:本题考查了分式的加减法,分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程(x+4)(x-4)=0的根是( )
| A、4 | B、-4 | C、±4 | D、±8 |
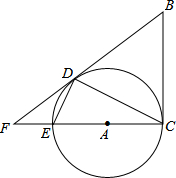 在Rt△ABC中,∠C=90°,BC=6,AC=3,过点B作以点A为圆心,AC为半径的⊙A的切线,切点为D,延长CA交圆于点E,交切线BD的延长线于点F,连接DE.
在Rt△ABC中,∠C=90°,BC=6,AC=3,过点B作以点A为圆心,AC为半径的⊙A的切线,切点为D,延长CA交圆于点E,交切线BD的延长线于点F,连接DE.  如图,AB∥CD,DA平分∠BDC,DE⊥AD,∠ABD=108°,求∠A和∠BDE的度数.
如图,AB∥CD,DA平分∠BDC,DE⊥AD,∠ABD=108°,求∠A和∠BDE的度数.