Question

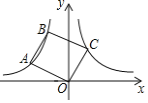
【题目】如图，已知二次函数y＝﹣x2+bx﹣c，它与x轴交于A、B，且A、B位于原点两侧，与y的正半轴交于C，顶点D在y轴右侧的直线l：y＝4上，则下列说法：①bc＜0；②0＜b＜4；③AB＝4；④S△ABD＝8．其中正确的结论有（ ）

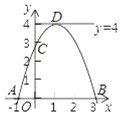
A.①②B.②③C.①②③D.①②③④

Answer 1

【答案】D

【解析】

先由抛物线解析式得到a=-1＜0，利用抛物线的对称轴得到b=-2a＜0，易得c＜0，于是可对①进行判断；由顶点D在y轴右侧的直线l：y=4上可得b的范围，从而可判断②是否正确；由a=-1及顶点D在y轴右侧的直线：y=4上，可得抛物线与x轴两交点之间的距离AB为定值，故可取b=2进行计算，即可求得AB的长度及S△ABD的大小．

∵抛物线开口向下，

∴＜0，

∵抛物线的对称轴为直线＞0，

∴b＞0，

而抛物线与y轴的交点在轴上方，

∴＞0，则c＜0，

∴bc＜0，故①正确；

由顶点D在y轴右侧的直线l：y=4上可得：

，

∴，

∵，

∴，

∴，

∴，

∴，

∴②正确；

∵，

∴该抛物线的开口方向及大小是一定的，

又∵顶点D在y轴右侧的直线：y=4上，

∴该抛物线与x轴两交点之间的距离AB是定值，

故令，

则，

此时抛物线解析式为：，

由，

得x1=﹣1，x2=3，

故AB=4，

∴③正确；

S△ABD=，

故④正确；

综上，①②③④均正确，

故选：D．