题目内容
11. 如图,已知⊙O是Rt△ABC的外接圆,∠ACB=90°,AC平分∠BAD,CD⊥AD于D,AD交⊙O于E.
如图,已知⊙O是Rt△ABC的外接圆,∠ACB=90°,AC平分∠BAD,CD⊥AD于D,AD交⊙O于E.(1)求证:CD为⊙O的切线;
(2)若⊙O的直径为8cm,CD=2$\sqrt{3}$cm,求弦AE的长.
分析 (1)连接OC,由等腰三角形的性质和角平分线得出∠2=∠3,证出∴OC∥AD,再由已知条件得出CD⊥OC,即可得出结论;
(2)作OF⊥AE于F,则AF=$\frac{1}{2}$AE,四边形OFDC是矩形,得出OF=CD=2$\sqrt{3}$cm,由勾股定理求出AF,即可得出AE的长.
解答 (1)证明: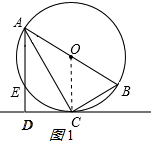 连接OC,如图所示:
连接OC,如图所示:
∵OA=OC,
∴∠1=∠3,
∵AC平分∠BAD,
∴∠1=∠2,
∴∠2=∠3,
∴OC∥AD,
∵CD⊥AD,
∴CD⊥OC,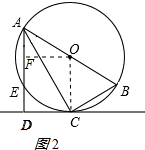
∴CD为⊙O的切线;
(2)解:作OF⊥AE于F,如图2所示:
则AF=$\frac{1}{2}$AE,四边形OFDC是矩形,
∴OF=CD=2$\sqrt{3}$cm,
∵OA=$\frac{1}{2}$AB=4cm,
∴AF=$\sqrt{O{A}^{2}-O{F}^{2}}$=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2,
∴AE=2AF=4.
点评 本题考查了切线的判定、等腰三角形的性质、平行线的判定与性质、矩形的判定与性质、垂径定理、勾股定理等知识;本题综合性强,熟练掌握切线的判定和垂径定理是解决问题的关键.

练习册系列答案
相关题目
6.下列图形中,是轴对称图形但不是中心对称图形的是( )
| A. | 平行四边形 | B. | 菱形 | C. | 正三角形 | D. | 圆 |
 已知:如图,点D是AB的中点,BC=$\frac{1}{3}AB$,DC=2,则AB的长为12.
已知:如图,点D是AB的中点,BC=$\frac{1}{3}AB$,DC=2,则AB的长为12. 如图所示,线段AB=14cm,C是AB上一点,且AC=9cm,O为AB的中点,线段OC的长度为2cm.
如图所示,线段AB=14cm,C是AB上一点,且AC=9cm,O为AB的中点,线段OC的长度为2cm.
 如图,AB⊥BC,AD⊥DC,∠BAD=100°,在BC、CD上分别找一点M、N,当△AMN的周长最小时,∠AMN+∠ANM的度数是160°.
如图,AB⊥BC,AD⊥DC,∠BAD=100°,在BC、CD上分别找一点M、N,当△AMN的周长最小时,∠AMN+∠ANM的度数是160°. 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE所叠得△DFE,延长EF交边AB于点G,连接DG,BF,给出以下结论:
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE所叠得△DFE,延长EF交边AB于点G,连接DG,BF,给出以下结论: