题目内容
等腰△ABC的周长为16,底边BC上的高为4,则△ABC的面积是
12
12
.分析:设底边长为2x.则根据等腰三角形的周长公式可以求得腰长为(8-x).然后由等腰三角形“三合一”的性质、勾股定理可以列出关于x的方程(8-x)2=x2+42,通过解方程可以求得x=3,所以由三角形的面积公式可以填空.
解答: 解:设底边长为2x.
解:设底边长为2x.
∴腰长为
=8-x.
利用勾股定理:(8-x)2=x2+42,
∴x=3,
∴△ABC面积为
×6×4=12.
故答案是:12.
 解:设底边长为2x.
解:设底边长为2x.∴腰长为
| 16-2x |
| 2 |
利用勾股定理:(8-x)2=x2+42,
∴x=3,
∴△ABC面积为
| 1 |
| 2 |
故答案是:12.
点评:本题考查了勾股定理、等腰三角形的性质.解题时,利用了等腰三角形的高线、中线重合的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
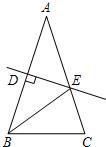 2、如图,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
2、如图,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( ) 20、如图,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,求△BEC的周长.
20、如图,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,求△BEC的周长.