Question

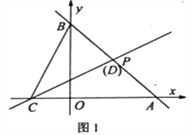
【题目】如图1，在正方形ABCD中，点E为AD上一点，FG⊥CE分别交AB、CD于F、G，垂足为O．

（1）求证：CE=FG；

（2）如图2，连接OB，若AD=3DE，∠OBC=2∠DCE。

求的值；

若AD=3，则OE的长为_________（直接写出结果）．

Answer 1

【答案】

【解析】（1）过点B作BM∥FG交CD于M ,构造三角形，证△BCM≌△CDE，可得; CE=BM=FG;(2) 过点B作BM∥FG交CD于M , 连接MO，由（1）证BC=BO，再证MC=MO=MG=ED，又AD＝3DE，所以；（3）由(1)(2)可得DE=OM=1,BO=AD=3,

又BM=CE=，再根据面积公式得OC=2×.

（1）过点B作BM∥FG交CD于M ,

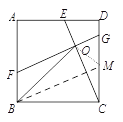
易证四边形FBMG为平行四边形

∴FG=BM，

由BC=CD;∠BCM=∠CDE;∠MBC=∠ECD

可证△BCM≌△CDE，

∴CE=BM=FG；

（2）过点B作BM∥FG交CD于M ,

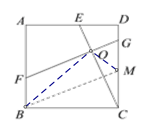
由（1）知△BCM≌△CDE，又∠OBC＝2∠DCE ,

MC=ED，∠MBC＝∠DCE＝∠MBO，

由BM∥FG得MB⊥CE，

∴∠BOC＝∠BCO，

∴BC=BO，连接MO，

∴BM垂直平分OC，

∴MC=MO，

又∵∠GOM=∠BMO=∠BMC=∠OGM

∴MC=MO=MG=ED，

又AD＝3DE，

∴；

（3）∵AD=3，

∴由(1)(2)可得

DE=OM=1,BO=AD=3,∴BM=CE= ,

OC=2× =2×= ,

∴OE=CE-CO＝.