题目内容
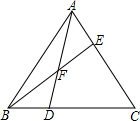
如图,已知在平行四边形ABCD中,对角线AC和BD相交于点O.在BC上取点E,使EC=
BC,DE和AC相交于点F.求AO:OF:FC?

| 1 |
| 4 |

取DE中点G,连接OG,
∵四边形ABCD是平行四边形,
∴BO=DO,
∴OG=
BE,OG∥BE,
∵EC=
BC,
∴EC=
BE,
∴EC=
OG.
∵OG∥BC,
∴
=
=
,
∴AO:OF:FC=5:3:2.

∵四边形ABCD是平行四边形,
∴BO=DO,
∴OG=
| 1 |
| 2 |
∵EC=
| 1 |
| 4 |
∴EC=
| 1 |
| 3 |
∴EC=
| 2 |
| 3 |
∵OG∥BC,
∴
| CF |
| OF |
| EC |
| OG |
| 2 |
| 3 |
∴AO:OF:FC=5:3:2.


练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目