题目内容
给定下列条件,不能判定三角形是直角三角形的是
- A.∠A:∠B:∠C=1:2:3
- B.∠A+∠B=∠C
- C.∠A=
 ∠B=
∠B= ∠C
∠C - D.∠A=2∠B=3∠C
D
分析:根据三角形的内角和等于180°求出最大角,然后选择即可.
解答:A、最大角∠C= ×180°=90°,是直角三角形,不符合题意;
×180°=90°,是直角三角形,不符合题意;
B、最大角∠C=180°÷2=90°,是直角三角形,不符合题意;
C、设∠A=x,则∠B=2x,∠C=3x,
所以,x+2x+3x=180°,
解得x=30°,
最大角∠C=3×30°=90°,是直角三角形,不符合题意;
D、设∠A=x,则∠B= x,∠C=
x,∠C= x,
x,
所以,x+ x+
x+ x=180°,
x=180°,
解得x=180°×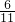 >90°,是钝角三角形,符合题意.
>90°,是钝角三角形,符合题意.
故选D.
点评:本题考查了三角形的内角和定理,求出各选项中的最大角是解题的关键.
分析:根据三角形的内角和等于180°求出最大角,然后选择即可.
解答:A、最大角∠C=
 ×180°=90°,是直角三角形,不符合题意;
×180°=90°,是直角三角形,不符合题意;B、最大角∠C=180°÷2=90°,是直角三角形,不符合题意;
C、设∠A=x,则∠B=2x,∠C=3x,
所以,x+2x+3x=180°,
解得x=30°,
最大角∠C=3×30°=90°,是直角三角形,不符合题意;
D、设∠A=x,则∠B=
 x,∠C=
x,∠C= x,
x,所以,x+
 x+
x+ x=180°,
x=180°,解得x=180°×
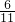 >90°,是钝角三角形,符合题意.
>90°,是钝角三角形,符合题意.故选D.
点评:本题考查了三角形的内角和定理,求出各选项中的最大角是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
光明中学数学活动小组为了调查居民的用水情况,从某社区的500户家庭中随机抽取了20户家庭的月用水量,结果如下表所示:
| 月用水量(吨) | 10 | 15 | 20 | 25 |
| 户数 | 8 | 6 | 4 | 2 |
(2)根据上述数据,试估计该社区的月用水量.
 如图,l1表示名湖商场一天的彩电销售额与销售量的关系,l2表示该公司一天的销售成本与彩电销售量的关系.
如图,l1表示名湖商场一天的彩电销售额与销售量的关系,l2表示该公司一天的销售成本与彩电销售量的关系. 图象交于A、B两点,则当x取何值时,正比例函数的值大于反比例函数的值?
图象交于A、B两点,则当x取何值时,正比例函数的值大于反比例函数的值? ,则黄球有________个.
,则黄球有________个. 互为相反数,则
互为相反数,则 =________.
=________.