题目内容
在直角坐标系中，O为坐标原点，点A的坐标为（2，2），点C是线段OA上的一个动点（不运动至O，A两点），过点C作CD⊥x轴，垂足为D，以CD为边在右侧作正方形CDEF. 连接AF并延长交x轴的正半轴于点B，连接OF,设OD＝t.
⑴ 求tan∠FOB的值；
⑵用含t的代数式表示△OAB的面积S；
⑶是否存在点C, 使以B，E，F为顶点的三角形与△OFE相似，若存在，请求出所有满足要求的B点的坐标；若不存在，请说明理由．
 |
答案：解：(1)∵A(2,2) ∴∠AOB=45°
∴CD=OD=DE=EF= ∴
……………………（2分）
(2)由△ACF～△AOB得
∴
∴
……………………（4分）
(3)要使△BEF与△OFE相似,∵∠FEO=∠FEB=90°
∴只要
或
即:
或
① 当时, 
,
∴
∴
(舍去)或
∴B(6,0) …………………（2分）
② 当时,
(ⅰ)当B在E的左侧时,
,
∴
∴(舍去)或
∴B(1,0) ……………（2分）
(ⅱ)当B在E的右侧时,
,
∴
∴(舍去)或
∴B(3,0) ……………（2分）
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
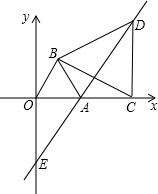OAB，C为x轴正半轴上的一个动点（OC＞1），连接BC，以BC为边在第一象限内作等边△BCD，直线DA交y轴于E点．
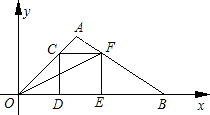在直角坐标系中，O为坐标原点，点A的坐标为（2，2），点C是线段OA上的一个动点（不运动至O，A两点），过点C作CD⊥x轴，垂足为D，以CD为边在右侧作正方形CDEF．连接AF并延长交x轴的正半轴于点B，连接OF，设OD=t．
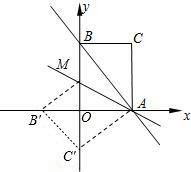点B′处，C的对应点为C′．