��Ŀ����
 ��ֱ������ϵ�У�OΪ����ԭ�㣬��A������Ϊ��2��2������C���߶�OA�ϵ�һ�����㣨���˶���O��A���㣩������C��CD��x�ᣬ����ΪD����CDΪ�����Ҳ���������CDEF������AF���ӳ���x����������ڵ�B������OF����OD=t��
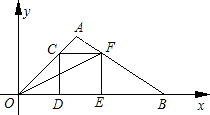
��ֱ������ϵ�У�OΪ����ԭ�㣬��A������Ϊ��2��2������C���߶�OA�ϵ�һ�����㣨���˶���O��A���㣩������C��CD��x�ᣬ����ΪD����CDΪ�����Ҳ���������CDEF������AF���ӳ���x����������ڵ�B������OF����OD=t����1����tan��FOB��ֵ��
��2���ú�t�Ĵ���ʽ��ʾ��OAB�����S��
��3���Ƿ���ڵ�B��ʹ��B��E��FΪ��������������OFE���ƣ������ڣ��������������Ҫ���B������ꣻ�������ڣ���˵�����ɣ�
��������1����֪��A�����꣬���Ƴ�CD=OD=DE=EF=t�������tan��FOB��
��2��֤����ACF�ס�AOB�Ƴ���
=
��Ȼ�����OB����t�ĵ�����ϵʽ���̶����S��OAB��ֵ��
��3��������Ҫʹ��BEF�ס�OFE����Ҫ
=
��
=
������BE=2t��EB=
t���������𣮵�BE=2tʱ��BO=4t�������������߶α����tֵ����EB=
tʱҲҪϸ�������������B��E���Ҳ��Լ���B��E�����ʱOB��ȡֵ�������߶α����tֵ��
��2��֤����ACF�ס�AOB�Ƴ���
2
| ||||
2
|
| t |
| OB |
��3��������Ҫʹ��BEF�ס�OFE����Ҫ
| OE |
| EB |
| EF |
| EF |
| OE |
| EF |
| EF |
| EB |
| 1 |
| 2 |
| 1 |
| 2 |
����⣺��1����A��2��2����
���AOB=45�㣬
��CD=OD=DE=EF=t��
��tan��FOB=
=
����3�֣�
��2����CF��OB��
���ACF�ס�AOB��
��
=
��
��OB=
��
��S��OAB=
(0��t��2)����4�֣�
��3��Ҫʹ��BEF���OFE���ƣ�
�ߡ�FEO=��FEB=90�㣬
��ֻҪ
=
��
=
��
����BE=2t��EB=
t��
�ٵ�BE=2tʱ��BO=4t��
��
=4t��
��t1=0����ȥ����t2=
��
��B��6��0������2�֣�
�ڵ�EB=
tʱ��
��������B��E�����ʱ��

OB=OE-EB=
t��
��
=
t��
��t1=0����ȥ����t2=
��
��B��1��0������2�֣�
��������B��E���Ҳ�ʱ��OB=OE+EB=
t��
��
=
t��
��t1=0����ȥ����t2=
��
��B��3��0������2�֣�
���ϣ�B��1��0����3��0����6��0����
���AOB=45�㣬
��CD=OD=DE=EF=t��
��tan��FOB=
| t |
| 2t |
| 1 |
| 2 |
��2����CF��OB��
���ACF�ס�AOB��
��
2
| ||||
2
|
| t |
| OB |
��OB=
| 2t |
| 2-t |
��S��OAB=
| 2t |
| 2-t |
��3��Ҫʹ��BEF���OFE���ƣ�
�ߡ�FEO=��FEB=90�㣬
��ֻҪ
| OE |
| EB |
| EF |
| EF |
| OE |
| EF |
| EF |
| EB |
����BE=2t��EB=
| 1 |
| 2 |
�ٵ�BE=2tʱ��BO=4t��
��
| 2t |
| 2-t |
��t1=0����ȥ����t2=
| 3 |
| 2 |
��B��6��0������2�֣�
�ڵ�EB=
| 1 |
| 2 |
��������B��E�����ʱ��

OB=OE-EB=
| 3 |
| 2 |
��
| 2t |
| 2-t |
| 3 |
| 2 |
��t1=0����ȥ����t2=
| 2 |
| 3 |
��B��1��0������2�֣�
��������B��E���Ҳ�ʱ��OB=OE+EB=
| 5 |
| 2 |
��
| 2t |
| 2-t |
| 5 |
| 2 |
��t1=0����ȥ����t2=
| 6 |
| 5 |
��B��3��0������2�֣�
���ϣ�B��1��0����3��0����6��0����
���������⿼����������ε����ʣ�������ͼ�ε������Լ����������ε��ж����й�֪ʶ��

��ϰ��ϵ�д�
�����Ŀ
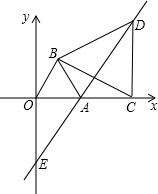 OAB��CΪx���������ϵ�һ�����㣨OC��1��������BC����BCΪ���ڵ�һ���������ȱߡ�BCD��ֱ��DA��y����E�㣮
OAB��CΪx���������ϵ�һ�����㣨OC��1��������BC����BCΪ���ڵ�һ���������ȱߡ�BCD��ֱ��DA��y����E�㣮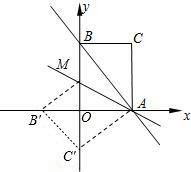 ��B�䴦��C�Ķ�Ӧ��ΪC�䣮
��B�䴦��C�Ķ�Ӧ��ΪC�䣮