题目内容
在直角坐标系中，O为坐标原点，△ABO是正三角形，若点B的坐标是（-2，0），则点A的坐标是
(-1，
)，(-1，-
)
| 3 |
| 3 |
(-1，
)，(-1，-
)
．| 3 |
| 3 |
分析：首先根据题意画出图形，过点A作AC⊥OB于点C，由△ABO是正三角形，点B的坐标是（-2，0），即可求得OC与AC的长，继而求得答案．
解答：
解：如图，过点A作AC⊥OB于点C，
∵△OAB是正三角形，
∴OA=OB=2，OC=BC=
OB=1，
∴AC=
=
，
∴点A的坐标是；（-1，
），
同理：点A′的坐标是（-1，-
），
∴点A的坐标是（-1，
）或（-1，-
）．
故答案为：（-1，
）或（-1，-
）．
解：如图，过点A作AC⊥OB于点C，∵△OAB是正三角形，
∴OA=OB=2，OC=BC=
| 1 |
| 2 |
∴AC=
| OA2-OC2 |
| 3 |
∴点A的坐标是；（-1，
| 3 |
同理：点A′的坐标是（-1，-
| 3 |
∴点A的坐标是（-1，
| 3 |
| 3 |
故答案为：（-1，
| 3 |
| 3 |
点评：此题考查了等边三角形的性质与勾股定理．此题难度不大，注意掌握数形结合思想与分类讨论思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
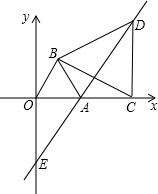OAB，C为x轴正半轴上的一个动点（OC＞1），连接BC，以BC为边在第一象限内作等边△BCD，直线DA交y轴于E点．
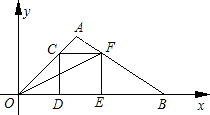在直角坐标系中，O为坐标原点，点A的坐标为（2，2），点C是线段OA上的一个动点（不运动至O，A两点），过点C作CD⊥x轴，垂足为D，以CD为边在右侧作正方形CDEF．连接AF并延长交x轴的正半轴于点B，连接OF，设OD=t．
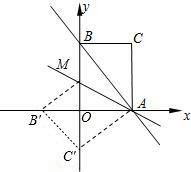点B′处，C的对应点为C′．