题目内容
 如图,在Rt△ABC中,∠BAC=90°,AB=8,AC=6,线段AB为半圆O的直径,将Rt△ABC沿射线AB方向平移,使斜边与半圆O相切于点G,得△DEF,DF与BC交于点H,则Rt△ABC与△DEF重叠(阴影)部分的面积为
如图,在Rt△ABC中,∠BAC=90°,AB=8,AC=6,线段AB为半圆O的直径,将Rt△ABC沿射线AB方向平移,使斜边与半圆O相切于点G,得△DEF,DF与BC交于点H,则Rt△ABC与△DEF重叠(阴影)部分的面积为考点:切线的性质,平移的性质
专题:
分析:连接OG,先根据勾股定理计算出BC=5,再根据平移的性质得AD=BE,DF=AC=6,EF=BC=10,∠EDF=∠BAC=90°,由于EF与半圆O相切于点G,根据切线的性质得OG⊥EF,然后证明Rt△EOG∽Rt△EFD,利用相似比可计算出OE=
,所以BE=OE-OB=
,然后求出BD的长度,然后利用相似比例式求出DH的长度,从而求出△BDH,即阴影部分的面积.
| 20 |
| 3 |
| 8 |
| 3 |
解答:
解:连结OG,如图,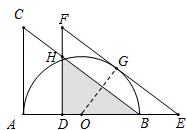
∵∠BAC=90°,AB=8,AC=6,
∴BC=
=10,
∵Rt△ABC沿射线AB方向平移,使斜边与半圆O相切于点G,得△DEF,
∴AD=BE,DF=AC=6,EF=BC=10,∠EDF=∠BAC=90°,
∵EF与半圆O相切于点G,
∴OG⊥EF,
∵AB=8,线段AB为半圆O的直径,
∴OB=OG=4,
∵∠GEO=∠DEF,
∴Rt△EOG∽Rt△EFD,
∴
=
,即
=
,解得OE=
,
∴BE=OE-OB=
-4=
;
∴BD=DE-BE=8-
=
.
∵DF∥AC,
∴△ABC∽△DBH,
∴
=
,即
=
,
解得:DH=4.
∴S阴影=S△BDH=
BD•DH=
×
×4=
,
即Rt△ABC与△DEF重叠(阴影)部分的面积为
.
故答案为
.

∵∠BAC=90°,AB=8,AC=6,
∴BC=
| AB2+AC2 |
∵Rt△ABC沿射线AB方向平移,使斜边与半圆O相切于点G,得△DEF,
∴AD=BE,DF=AC=6,EF=BC=10,∠EDF=∠BAC=90°,
∵EF与半圆O相切于点G,
∴OG⊥EF,
∵AB=8,线段AB为半圆O的直径,
∴OB=OG=4,
∵∠GEO=∠DEF,
∴Rt△EOG∽Rt△EFD,
∴
| OE |
| EF |
| OG |
| DF |
| OE |
| 10 |
| 4 |
| 6 |
| 20 |
| 3 |
∴BE=OE-OB=
| 20 |
| 3 |
| 8 |
| 3 |
∴BD=DE-BE=8-
| 8 |
| 3 |
| 16 |
| 3 |
∵DF∥AC,
∴△ABC∽△DBH,
∴
| DH |
| AC |
| BD |
| AB |
| DH |
| 6 |
| ||
| 8 |
解得:DH=4.
∴S阴影=S△BDH=
| 1 |
| 2 |
| 1 |
| 2 |
| 16 |
| 3 |
| 32 |
| 3 |
即Rt△ABC与△DEF重叠(阴影)部分的面积为
| 32 |
| 3 |
故答案为
| 32 |
| 3 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了平移的性质、勾股定理和相似三角形的判定与性质.

练习册系列答案
相关题目
下列计算正确的是( )
A、
| ||||||
| B、(a+b)2=a2+b2 | ||||||
| C、a5+a5=a10 | ||||||
| D、a-1+2a-1=3a-1 |
 电子绳游戏盘是如图所示的△ABC,AB=6,AC=7,BC=8.如果跳蚤开始时在BC边的P0处,BP0=2,跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2010与P2013之间的距离为( )
电子绳游戏盘是如图所示的△ABC,AB=6,AC=7,BC=8.如果跳蚤开始时在BC边的P0处,BP0=2,跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2010与P2013之间的距离为( ) 如图,△ABC中,∠BAC=90°,AH是高,BD平分∠ABC交AH于E,DF⊥BC于F,试说明四边形AEFD是菱形.
如图,△ABC中,∠BAC=90°,AH是高,BD平分∠ABC交AH于E,DF⊥BC于F,试说明四边形AEFD是菱形.