题目内容
如图所示，已知边长为2的正三角形ABC中，P0是BC边的中点，一束光线自P0发出射到AC上的P1后，依次反射到AB、BC上的点P2和P3，且1＜BP3＜
（反射角等于入射角），则P1C的取值范围是________．
1＜P1C＜
分析：首先利用光的反射定律及等边三角形的性质证明△P0P1C∽△P2P1A∽△P2P3B，再根据相似三角形对应边成比例得到用含P3B的代数式表示P1C的式子，然后由
1＜BP3＜，即可求出P1C长的取值范围．
解答：∵反射角等于入射角，
∴∠P0P1C=∠P2P1A=∠P2P3B，
又∵∠C=∠A=∠B=60°，
∴△P0P1C∽△P2P1A∽△P2P3B，
∴
=
=
，
设P1C=x，P2A=y，则P1A=2-x，P2B=2-y．
∴
=
=
，
∴
，
∴x=
（2+P3B）．
又∵1＜BP3＜，
∴1＜x＜，
即P1C长的取值范围是：1＜P1C＜．
故答案为1＜P1C
．
点评：本题主要考查了等边三角形的性质，在解题时要根据等边三角形的性质找出对应点是解此题的关键，难度较大．
分析：首先利用光的反射定律及等边三角形的性质证明△P0P1C∽△P2P1A∽△P2P3B，再根据相似三角形对应边成比例得到用含P3B的代数式表示P1C的式子，然后由
1＜BP3＜
，即可求出P1C长的取值范围．解答：∵反射角等于入射角，
∴∠P0P1C=∠P2P1A=∠P2P3B，
又∵∠C=∠A=∠B=60°，
∴△P0P1C∽△P2P1A∽△P2P3B，
∴
==，设P1C=x，P2A=y，则P1A=2-x，P2B=2-y．
∴
==，∴
，∴x=
（2+P3B）．又∵1＜BP3＜
，∴1＜x＜
，即P1C长的取值范围是：1＜P1C＜
．故答案为1＜P1C
．点评：本题主要考查了等边三角形的性质，在解题时要根据等边三角形的性质找出对应点是解此题的关键，难度较大．
练习册系列答案
相关题目
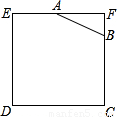
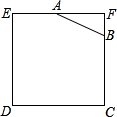如图所示，已知边长为4的正方形钢板有一个角锈蚀，其中AF=2，BF=1，为了合理利用这块钢板．将在五边形EABCD内截取一个矩形块MDNP，使点P在AB上，且要求面积最大，求钢板的最大利用率．
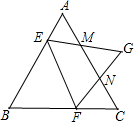等边△EFG，直线EG，FG交直线AC于点M，N，
如图所示，已知边长为2的正三角形ABC中，P0是BC边的中点，一束光线自P0发出射到AC上的P1后，依次反射到AB、BC上的点P2和P3，且1＜BP3＜
如图所示，已知边长为a的等边三角形ABC，两顶点A，分别在x轴，y轴的正半轴上滑动，连接OC，则OC长的最大值是