题目内容
如图∠B=90°,AB=16cm,BC=12cm,AD=21cm,CD=29cm,求四边形ABCD的面积.
分析:先根据△ABC是直角三角形求出AC的长,再根据△ACD各边的长判断出△ACD是直角三角形,
再利用S四边形ABCD=S△ABC=S△ACD解答.
再利用S四边形ABCD=S△ABC=S△ACD解答.
解答:解:∵△ABC中,∠B=90°,AB=16cm,BC=12cm,
∴AC=
=
=20cm,
∵△ACD中,AD=21cm,CD=29cm,AC=20cm,212+202=841=292,
∴△ACD是直角三角形,
∴S四边形ABCD=S△ABC+S△ACD
=
AB•BC+
AD•AC
=
×16×12+
×21×20
=306cm2.
∴AC=
| AB2+BC2 |
| 162+122 |
∵△ACD中,AD=21cm,CD=29cm,AC=20cm,212+202=841=292,
∴△ACD是直角三角形,
∴S四边形ABCD=S△ABC+S△ACD
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=306cm2.
点评:本题考查的是勾股定理、勾股定理的逆定理及三角形的面积,熟练掌握以上知识点是解答此题的关键.

练习册系列答案
相关题目
 已知如图∠B=90°AB=AD=BC,DE⊥AC,求证:BE=DC.
已知如图∠B=90°AB=AD=BC,DE⊥AC,求证:BE=DC. 14、如图∠XOY=90°,点A,B分别在射线OX,OY上移动,∠OAB的内角平分线与∠OBA的外角平分线交于点C,试问∠ACB的大小是否变动?为什么?
14、如图∠XOY=90°,点A,B分别在射线OX,OY上移动,∠OAB的内角平分线与∠OBA的外角平分线交于点C,试问∠ACB的大小是否变动?为什么?

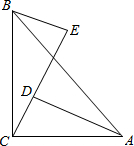 如图∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,
如图∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,