Question

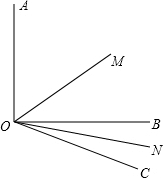
如图所示已知∠AOB=90°，∠BOC=30°，OM平分∠AOC，ON平分∠BOC．
（1）∠MON=

 

°；
（2）如图∠AOB=90°，将OC绕O点向下旋转，使∠BOC=2x°，仍然分别作∠AOC，∠BOC的平分线OM，ON，能否求出∠MON的度数？若能，求出其值；若不能，试说明理由；
（3）∠AOB=α，∠BOC=β，仍然分别作∠AOC，∠BOC的平分线OM，ON，能否求出∠MON的度数？若能，求∠MON的度数；并从你的求解中看出什么规律吗？

Answer 1

分析：（1）根据角平分线的以求出∠MOC与∠NOC的度数，然后相减即可求出∠MON的度数；
（2）根据（1）的求解思路，先利用角平分线的定义表示出∠MOC与∠NOC的度数，然后相减即可得到∠MON的度数；
（3）根据前两题的求解思路把具体数据换为α、β，然后整理即可得出规律．

解答：解：（1）∵∠AOB=90°，∠BOC=30°，
∴∠AOC=∠AOB+∠BOC=90°+30°=120°，
∵OM平分∠AOC，ON平分∠BOC，
∴∠MOC=

1

2

∠AOC=

1

2

×120°=60°，
∠NOC=

1

2

∠BOC=

1

2

×30°=15°，
∴∠MON=∠MOC-∠NOC=60°-15°=45°；（3分）

（2）能．
∵∠AOB=90°，∠BOC=2x°，
∴∠AOC=90°+2x°，（4分）
∵OM、ON分别平分∠AOC，∠BOC，
∴∠MOC=

1

2

∠AOC=

1

2

（90°+2x°）=45°+x，
∴∠CON=

1

2

∠BOC=x，（5分）
∴∠MON=∠MOC-∠CON=45°+x-x=45°；（6分）

（3）能．
∵∠AOB=α，∠BOC=β，
∴∠AOC=α+β，（7分）
∵OM、ON分别平分∠AOC，∠BOC，
∴∠MOC=

1

2

∠AOC=

1

2

（α+β），
∠CON=

1

2

∠BOC=

1

2

β，（8分）
∴∠MON=∠MOC-∠CON=

1

2

（α+β）-

1

2

β=

1

2

α，
即∠MON=

1

2

α．（9分）

点评：本题考查了角的计算，角平分线的定义，读懂题意，看懂题目图形找准解题思路是解题的关键，此类题目通常都是各小题都用同一个解题思路，所以准确确定思路比较关键．