题目内容
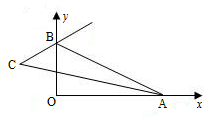 14、如图∠XOY=90°,点A,B分别在射线OX,OY上移动,∠OAB的内角平分线与∠OBA的外角平分线交于点C,试问∠ACB的大小是否变动?为什么?
14、如图∠XOY=90°,点A,B分别在射线OX,OY上移动,∠OAB的内角平分线与∠OBA的外角平分线交于点C,试问∠ACB的大小是否变动?为什么?分析:由∠OAB的内角平分线与∠OBA的外角平分线交于点C,得∠3=∠4,∠1=∠2,再利用三角形的外角性质得∠1=∠C+∠3①,∠1+∠2=90°+∠3+∠4,即2∠1=90°+2∠3②,把①×2-②得,2∠C-90°=0,即可求出∠C的度数.由此判断∠ACB的大小不变动.
解答: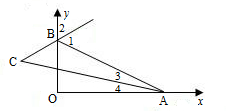 解:∠ACB的大小不变动,为45°.理由如下:
解:∠ACB的大小不变动,为45°.理由如下:
如图,
∵AC平分∠OAB,
∴∠3=∠4,
又∵BC平分∠OBA的外角,
∴∠1=∠2,
而∠1=∠C+∠3①,
∠1+∠2=90°+∠3+∠4,即2∠1=90°+2∠3②,
①×2-②得,2∠C-90°=0,
所以∠C=45°.
 解:∠ACB的大小不变动,为45°.理由如下:
解:∠ACB的大小不变动,为45°.理由如下:如图,
∵AC平分∠OAB,
∴∠3=∠4,
又∵BC平分∠OBA的外角,
∴∠1=∠2,
而∠1=∠C+∠3①,
∠1+∠2=90°+∠3+∠4,即2∠1=90°+2∠3②,
①×2-②得,2∠C-90°=0,
所以∠C=45°.
点评:本题考查了三角形的内角和定理:三角形的内角和为180°.同时考查了角平分线的性质和三角形外角性质.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 (2012•崇左)如图,已知∠XOY=90°,等边三角形PAB的顶点P与O点重合,顶点A是射线OX上的一个定点,另一个顶点B在∠XOY的内部.
(2012•崇左)如图,已知∠XOY=90°,等边三角形PAB的顶点P与O点重合,顶点A是射线OX上的一个定点,另一个顶点B在∠XOY的内部. (2013•嘉定区一模)在平面直角坐标系xOy中(如图),已知抛物线y=ax2+4ax+c(a≠0)经过A(0,4),B(-3,1),顶点为G.
(2013•嘉定区一模)在平面直角坐标系xOy中(如图),已知抛物线y=ax2+4ax+c(a≠0)经过A(0,4),B(-3,1),顶点为G.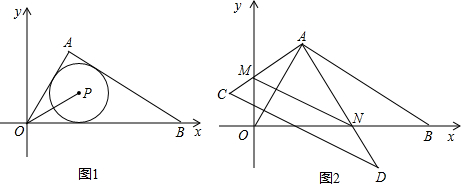
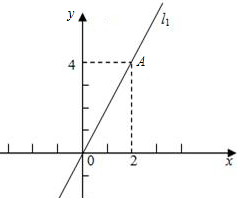 如图,在平面直角坐标系xoy中,直线l1经过点O和点A,将直线l1绕点O逆时针旋转90°,再向上平移2个单位长度得到直线l2.
如图,在平面直角坐标系xoy中,直线l1经过点O和点A,将直线l1绕点O逆时针旋转90°,再向上平移2个单位长度得到直线l2.