题目内容
在解方程组 时,甲同学正确解得
时,甲同学正确解得 乙同学把c看错了,而得到
乙同学把c看错了,而得到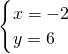 那么a,b,c的值为
那么a,b,c的值为
- A.a=-2,b=4,c=5
- B.a=4,b=5,c=-2
- C.a=5,b=4,c=2
- D.不能确定
B
分析:将甲同学的解代入方程组得到关于a与b的方程,并求出c的值,将乙同学的解代入方程组中第一个方程得到关于a与b的二元一次方程,联立组成关于a与b的方程组,求出方程组的解得到a与b的值即可.
解答:将 代入方程组得:3a+2b=22①,3c+14=8,即c=-2,
代入方程组得:3a+2b=22①,3c+14=8,即c=-2,
将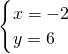 代入方程组中的第一个方程得:-2a+6b=22②,
代入方程组中的第一个方程得:-2a+6b=22②,
①×3-②得:11a=44,即a=4,
将a=4代入①得:12+2b=22,即b=5,
则a=4,b=5,c=-2.
故选B
点评:此题考查了二元一次方程组的解法,利用了消元的思想,消元的方法有:加减消元法与代入消元法.
分析:将甲同学的解代入方程组得到关于a与b的方程,并求出c的值,将乙同学的解代入方程组中第一个方程得到关于a与b的二元一次方程,联立组成关于a与b的方程组,求出方程组的解得到a与b的值即可.
解答:将
 代入方程组得:3a+2b=22①,3c+14=8,即c=-2,
代入方程组得:3a+2b=22①,3c+14=8,即c=-2,将
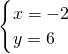 代入方程组中的第一个方程得:-2a+6b=22②,
代入方程组中的第一个方程得:-2a+6b=22②,①×3-②得:11a=44,即a=4,
将a=4代入①得:12+2b=22,即b=5,
则a=4,b=5,c=-2.
故选B
点评:此题考查了二元一次方程组的解法,利用了消元的思想,消元的方法有:加减消元法与代入消元法.

练习册系列答案
相关题目
两位同学在解方程组时,甲同学由
正确地解出
,乙同学因把c写错而错解
,那么a,b,c正确的值应为( )
|
|
|
| A、a=4,b=5,c=-1 |
| B、a=4,b=5,c=0 |
| C、a=4,b=5,c=-2 |
| D、a=4,b=5,c=2 |
两位同学在解方程组时,甲同学由
正确地解出
,乙同学因把C写错了解得
,那么a、b、c的正确的值应为( )
|
|
|
| A、a=4,b=5,c=-1 |
| B、a=4,b=5,c=-2 |
| C、a=-4,b=-5,c=0 |
| D、a=-4,b=-5,c=2 |
在解方程组 时,甲同学正确解得
时,甲同学正确解得 乙同学把
乙同学把 看错了,而得到
看错了,而得到 那么
那么 ,
,
 ,
, 的值为( )
的值为( )
 时,甲同学正确解得
时,甲同学正确解得 乙同学把
乙同学把 看错了,而得到
看错了,而得到 那么
那么 ,
,
 ,
, 的值为( )
的值为( )A. , , , , | B. , , , , | C. , , , ,  | D.不能确定 |
 时,甲同学正确解得
时,甲同学正确解得 乙同学把
乙同学把 看错了,而得到
看错了,而得到 那么
那么 ,
,  ,
, ,
, ,
, B.
B. ,
, ,
, C.
C. ,
, D.不能确定
D.不能确定