Question

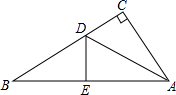在Rt△ABC中AC=9cm，BC=12cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合．求：
（1）AB=

15

cm，BE=

6

cm；
（2）设CD=x，则DE=

x

cm，BD=

（12-x）

cm；
（3）求CD的长及△BAD的面积．

Answer 1

分析：（1）在Rt△ABC中利用勾股定理即可算出AB的长，再根据折叠方法可得AC=AE，继而得到BE的长度；
（2）根据折叠方法可得CD=DE=xcm，则BD=（12-x）cm；
（3）根据（2）中线段的长度，在在Rt△BDE中利用勾股定理可得CD的长，进而得到DE的长，再利用三角形的面积公式即可算出△BAD的面积．

解答：解：（1）∵AC=9cm，BC=12cm，
∴AB=

AC2+BC2

=15（cm），
根据折叠方法可得：AC=AE=9cm，
∴BE=AB-AE=15-9=6（cm）；

（2）设CD=x，则DE=xcm，BD=（12-x）cm；

（3）在Rt△BDE中：BD²=BE²+DE²，
即：（12-x）²=6²+x²，
解得：x=

9

2

，
则CD=

9

2

cm，
△BAD的面积为：

1

2

•AB•DE=

1

2

×15×

9

2

=

135

4

（cm²）．

点评：此题主要考查了图形的折叠，以及勾股定理的应用，关键是找准折叠以后有哪些线段是对应相等的．