题目内容
在Rt△ABC中AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，求（1）AB的长；（2）CD的长．
分析：（1）在直角三角形中，知道两直角边，可直接应用勾股定理求得斜边的长度；
（2）可设CD=x，则BD=8-x，由AD为折痕，可得相等的线段，得到BE=AB-6，在直角三角形BED中应用勾股定理可求得CD的长．
（2）可设CD=x，则BD=8-x，由AD为折痕，可得相等的线段，得到BE=AB-6，在直角三角形BED中应用勾股定理可求得CD的长．
解答：解：（1）Rt△ABC中，AC=6cm，BC=8cm，
∴AB=
=
=10（cm）；
（2）设CD=x，则BD=8-x，
∵AD折痕，
∴DE=CD=x，AE=AC，
∴BE=AB-AE=10-6=4，
Rt△BDE中，
BD2=BE2+DE2，
∴（8-x）2=x2+42
解得x=3．
∴AB=
| AC2+BC2 |
| 62+82 |
（2）设CD=x，则BD=8-x，
∵AD折痕，
∴DE=CD=x，AE=AC，
∴BE=AB-AE=10-6=4，
Rt△BDE中，
BD2=BE2+DE2，
∴（8-x）2=x2+42
解得x=3．
点评：本题考查了翻折变换问题；找准相等的量，结合勾股定理求解是解答此类问题的关键．
练习册系列答案
相关题目
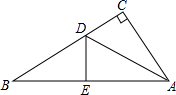在Rt△ABC中AC=9cm，BC=12cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合．求：
