题目内容
在Rt△ABC中AC=6，BC=8，则斜边上的中线CD=分析：根据勾股定理求出AB，再利用直角三角形中斜边上的中线等于斜边的一半求的CD的长，再利用BC为斜边得出CD的长．
解答：
解：Rt△ABC中，∠ACB=90°，当AC=6，BC=8为直角边，
∴AB2=AC2+BC2=82+62=100，
∴AB=10；
在Rt△ABC中，CD为斜边AB的中线，
∴CD=
AB（直角三角形斜边上的中线等于斜边的一半），
∴CD=5．
当BC为斜边，则斜边上的中线CD=4，
故答案是：5或4．
解：Rt△ABC中，∠ACB=90°，当AC=6，BC=8为直角边，∴AB2=AC2+BC2=82+62=100，
∴AB=10；
在Rt△ABC中，CD为斜边AB的中线，
∴CD=
| 1 |
| 2 |
∴CD=5．
当BC为斜边，则斜边上的中线CD=4，
故答案是：5或4．
点评：解答本题主要是运用了直角三角形的性质，即勾股定理和在直角三角形斜边上的中线等于斜边的一半．
练习册系列答案
相关题目
在Rt△ABC中AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，求（1）AB的长；（2）CD的长．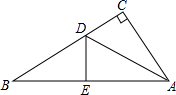
在Rt△ABC中AC=9cm，BC=12cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合．求：
