题目内容
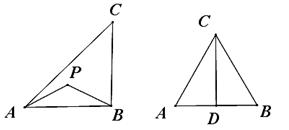
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心。
举例:如图1,若PA=PB,则点P为△ABC的准外心。
(1)应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且![]() ,
,
求∠APB的度数。
(2)探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长。

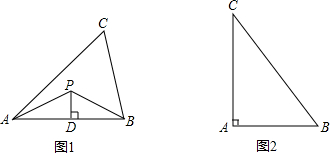
(1)解:⑴∵△ABC是等边三角形,CD是AB边上的高线
∴D为AB的中点。(等边三角形三线合一)
∴![]()
又∵![]()
∴AD=PD=BD
又∵CD是AB边上的高线
∴△ADP, △DBP为等腰直角三角形
∴∠APD=∠BPD=45
∴∠APB=∠APD+∠BPD=90°;(5分)
⑵∵BC=5,AB=3,∴AC=![]() ,
,
①若PB=PC,设PA=x,则![]() ,∴
,∴![]() ,即PA
,即PA![]() ,
,
②若PA=PC,则PA=2,
③若PA=PB,在Rt△PAB中,不可能
∴综上所述,PA=2或![]() (5分)
(5分)

练习册系列答案
相关题目
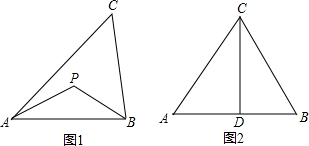

 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
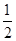 AB,求∠APB的度数。
AB,求∠APB的度数。