题目内容
 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.举例:如图,若PB=PC,则点P为△ABC的准外心.
已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上.求PA的长.(自己画图)
分析:先根据勾股定理求出AC的长度,根据准外心的定义,分①PB=PC,②PA=PC,③PA=PB三种情况,根据三角形的性质计算即可得解.
解答:解:∵BC=5,AB=3,
∴AC=
=
=4,
①若PB=PC,设PA=x,则x2+32=(4-x)2,
解得:x=
,即PA=
.
②若PA=PC,则PA=2.
③若PA=PB,由图知,在Rt△PAB中,不可能.
综上可得:PA=2或
.

∴AC=
| BC2-AB2 |
| 52-32 |
①若PB=PC,设PA=x,则x2+32=(4-x)2,
解得:x=
| 7 |
| 8 |
| 7 |
| 8 |
②若PA=PC,则PA=2.
③若PA=PB,由图知,在Rt△PAB中,不可能.
综上可得:PA=2或
| 7 |
| 8 |
点评:本题考查了勾股定理,等腰三角形的性质,读懂题意,弄清楚准外心的定义是解题的关键,根据准外心的定义,要注意分三种情况进行讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


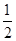 AB,求∠APB的度数。
AB,求∠APB的度数。