题目内容
（2013•江宁区二模）根据三角形外心的概念，我们可引入如下概念：定义：到三角形的两个顶点距离相等的点，叫做此三角形的准外心．
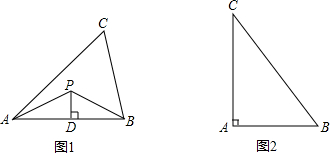
（1）应用：如图1，PA=PB，过准外心P作PD⊥AB，垂足为D，PD=
AB，求∠PAD；
（2）探究：如图2，在Rt△ABC中，∠A=90°，BC=10，AB=6，准外心P在AC边上，试探究PA的长．
（1）应用：如图1，PA=PB，过准外心P作PD⊥AB，垂足为D，PD=
| ||
| 6 |
（2）探究：如图2，在Rt△ABC中，∠A=90°，BC=10，AB=6，准外心P在AC边上，试探究PA的长．
分析：（1）根据PA=PB，PD⊥AB，得出AD=BD，求出PD=
AB，PD=
AD，再根据tan∠PAE=
=
，即可得出答案．
（2根据勾股定理求出AC的值，分三种情况进行讨论，若PB=PC，连结PB，设PA=x，得出PB=PC=8-x，再根据勾股定理求出PA的值；若PA=PC，得出PA=4；若PA=PB，由图知，不存在；从而得出PA的长．
| ||
| 6 |
| ||
| 3 |
| PD |
| AD |
| ||
| 3 |
（2根据勾股定理求出AC的值，分三种情况进行讨论，若PB=PC，连结PB，设PA=x，得出PB=PC=8-x，再根据勾股定理求出PA的值；若PA=PC，得出PA=4；若PA=PB，由图知，不存在；从而得出PA的长．
解答：
解：（1）∵PA=PB，PD⊥AB，
∴AD=BD，
∵PD=
AB，
∴PD=
AD，
在Rt△PAD中，tan∠PAE=
=
，
∴∠PAD=30°．
（2）在Rt△ABC中，
∵∠A=90°，BC=10，AB=6，
∴AC=
=
=8，
若PB=PC，连结PB，
设PA=x，则PB=PC=8-x，
在Rt△PAB中，
∵PB2=AP2+AB2，
∴（8-x）2=x2+62，
∴x=
，即PA=
，
若PA=PC，则PA=4，
若PA=PB，由图知，在Rt△PAB中，不可能，
故PA=4或
．
解：（1）∵PA=PB，PD⊥AB，∴AD=BD，
∵PD=
| ||
| 6 |
∴PD=
| ||
| 3 |
在Rt△PAD中，tan∠PAE=
| PD |
| AD |
| ||
| 3 |
∴∠PAD=30°．
（2）在Rt△ABC中，
∵∠A=90°，BC=10，AB=6，
∴AC=
| BC2-AB2 |
| 102-62 |
若PB=PC，连结PB，
设PA=x，则PB=PC=8-x，
在Rt△PAB中，
∵PB2=AP2+AB2，
∴（8-x）2=x2+62，
∴x=
| 7 |
| 4 |
| 7 |
| 4 |
若PA=PC，则PA=4，
若PA=PB，由图知，在Rt△PAB中，不可能，
故PA=4或
| 7 |
| 4 |
点评：此题考查了圆的综合，用到的知识点是勾股定理、特殊角的三角函数，等腰三角形的性质，注意解（2）时，要分三种情况讨论，不要漏项．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2013•江宁区二模）甲、乙两名同学在一次用频率去估计概率的实验中，统计了某一结果出现的频率绘出的统计图如图所示，则符合这一结果的实验可能是（ ）
（2013•江宁区二模）如图，若将木条a绕点O旋转后与木条b平行，则旋转角的最小值为
（2013•江宁区二模）在如图所示的5×5方格中，每个小方格都是边长为1的正方形，△ABC是格点三角形（即顶点恰好是正方形的顶点），将△ABC绕点A逆时针旋转90°，则在△ABC扫过的区域中（不含边界上的点），到点O的距离为无理数的格点的个数是（ ）