题目内容
8.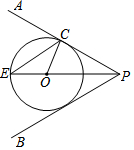 如图,∠OPA=$\frac{1}{2}$∠APB,⊙O与PA相切于点C.
如图,∠OPA=$\frac{1}{2}$∠APB,⊙O与PA相切于点C.(1)求证:直线PB与⊙O相切.
(2)PO的延长线与⊙O相交于点E,若⊙O的半径为3,PC=4,求CE的长.
分析 (1)连接OC,作OD⊥PB于D点.证明OD=OC即可.根据角的平分线性质易证;
(2)设PO交⊙O于F,连接CF.根据勾股定理得PO=5,则PE=8.证明△PCF∽△PEC,得CF:CE=PC:PE=1:2.根据勾股定理求解CE.
解答 (1)证明:连接OC,作OD⊥PB于D点.
∵⊙O与PA相切于点C,
∴OC⊥PA,
∵∠OPA=$\frac{1}{2}$∠APB,
∴点O在∠APB的平分线上,OC⊥PA,OD⊥PB,
∴OD=OC.
∴直线PB与⊙O相切;
(2)解:设PO交⊙O于F,连接CF.
∵OC=3,PC=4,
∴PO=5,PE=8.
∵⊙O与PA相切于点C,
∴∠PCF=∠E.
又∵∠CPF=∠EPC,
∴△PCF∽△PEC,
∴CF:CE=PC:PE=4:8=1:2.
∵EF是直径,
∴∠ECF=90°.
设CF=x,则EC=2x.
则x2+(2x)2=62,
解得x=$\frac{6\sqrt{5}}{5}$,
∴CE=$\frac{12\sqrt{5}}{5}$.
点评 此题考查了切线的判定、相似三角形的性质.注意:当不知道直线与圆是否有公共点而要证明直线是圆的切线时,可通过证明圆心到直线的距离等于圆的半径,来解决问题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
16.下列调查中,适宜采用抽样调查方式的是( )
| A. | 调查札幌亚冬会女子越野滑雪1.4公里决赛参赛运动员兴奋剂的使用情况 | |
| B. | 调查中国民众对美国在韩部署萨德系统持反对态度的比例 | |
| C. | 调查中国国产航母各零部件的质量 | |
| D. | 调查某班学生对感动中国2016年度人物我校高2004级校友秦珇飞的知晓率 |
 如图,正五边形ABCDE内接于⊙O,若⊙O的半径为5,则弧AB的长为2π.
如图,正五边形ABCDE内接于⊙O,若⊙O的半径为5,则弧AB的长为2π.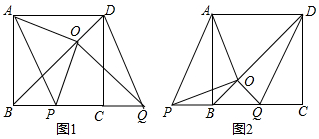
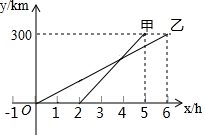 甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,乙出发2h后甲再出发,且甲、乙两人离A地的距离y甲、y乙与时间x之间的函数图象如图所示.
甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,乙出发2h后甲再出发,且甲、乙两人离A地的距离y甲、y乙与时间x之间的函数图象如图所示.