题目内容
7.已知正比例函数的图象上有一点P,它的纵坐标与横坐标的比值是-$\frac{5}{6}$.(1)求这个函数的解析式;
(2)点P1(10,-12),P2(-3,36)在这个函数的图象上吗?为什么?
分析 (1)设正比例函数的解析式为y=kx,根据题意得出k=$\frac{y}{x}$=-$\frac{5}{6}$,即可求得解析式;
(2)分别代入x=10和x=-3求得对应的函数值,与P1(10,-12),P2(-3,36)比较即可判断.
解答 解:(1)设正比例函数的解析式为y=kx,
∴k=$\frac{y}{x}$,
∵点P的纵坐标与横坐标的比值是-$\frac{5}{6}$.
∴k=-$\frac{5}{6}$,
∴正比例函数的解析式为y=-$\frac{5}{6}$x;
(2)∵当x=10时,y=-$\frac{5}{6}$×10=-$\frac{25}{3}$≠-12,当x=-3时,y=y=-$\frac{5}{6}$×(-3)=$\frac{5}{2}$≠36,
∴P1(10,-12),P2(-3,36)不在这个函数的图象上.
点评 本题考查了待定系数法求正比例函数的解析式以及一次函数图象上点的坐标特征,熟练掌握待定系数法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.下面四个关系式中,错误的是( )
| A. | 商品利润率=$\frac{商品利润}{商品进价}$×100% | |
| B. | 商品利润率=$\frac{商品利润}{商品售价}$×100% | |
| C. | 商品售价=商品进价×(1+利润率) | |
| D. | 商品利润=商品利润率×商品进价 |
15.反比例函数y=$\frac{2}{x}$的图象不经过的点是( )
| A. | (-1,-2) | B. | (-2,1) | C. | (1,2) | D. | (2,1) |
12.某地一天的最高气温是12℃,最低气温是-2℃,则该地这天的温差是( )
| A. | -10℃ | B. | 10℃ | C. | 14℃ | D. | -14℃ |
16.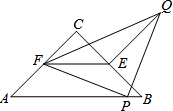 如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )
如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )
 如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )
如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
 已知:如图,BC∥EF,AD=BE,BC=EF,求证:(1)△ABC≌△DEF.(2)AC∥DF.
已知:如图,BC∥EF,AD=BE,BC=EF,求证:(1)△ABC≌△DEF.(2)AC∥DF.