题目内容
19.一农场要建一个长方形的养鸡场,养鸡场的一边靠墙(墙长25m),另三边用木栏围成,木栏的长为40m,(1)若养鸡场的面积能达到180m2,则养鸡场的长和宽各为多少?
(2)养鸡场的面积能达到250m2?
分析 (1)首先设平行于墙的一边为x米,则另一边长为$\frac{40-x}{2}$米,然后根据矩形的面积=长×宽,用未知数表示出鸡场的面积,根据面积为180m2,可得方程,解方程即可;
(2)要求鸡场的面积能否达到250平方米,只需让鸡场的面积先等于250,然后看得出的一元二次方程有没有实数根,如果有就证明可以达到250平方米,如果方程无解,说明不能达到250平方米.
解答 解:(1)设平行于墙的一边为x米,则另一边长为$\frac{40-x}{2}$米,根据题意得:
x•$\frac{40-x}{2}$=180,
整理得出:
x2-40x+360=0,
解得:x1=20+2$\sqrt{10}$,x2=20-2$\sqrt{10}$,
由于墙长25米,而20+2$\sqrt{10}$>25,
∴x1=20+2$\sqrt{10}$不合题意舍去,
∵0<20-2$\sqrt{10}$<25,
∴x2=20-2$\sqrt{10}$,符合题意,
此时$\frac{40-x}{2}$=10+$\sqrt{10}$,
答:此时鸡场平行于墙的一边长(20-2$\sqrt{10}$)米,宽是(10+$\sqrt{10}$)米.
(2)设与墙平行的一边长为x米,则:
x•$\frac{40-x}{2}$=250,
整理得出:x2-40x+500=0,
∵b2-4ac=402-4×1×500=-400<0,
∴此方程无解,
∴不能使鸡场的面积能达到250m2.
点评 此题主要考查了一元二次方程的应用,一元二次方程根的判别式的应用.读懂题意,找到等量关系准确的列出方程是解题的关键.

练习册系列答案
相关题目
4.下表是根据方程x2+3x-4=0所列:
则根据表中数据可以判断此方程的一个根是x=1.
| x | 0 | 1 | 2 | 3 | 4 |
| x2+3x-4 | -4 | 0 | 6 | 14 | 24 |
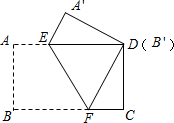 把一张长方形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,求:
把一张长方形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,求: