题目内容
如果x2+x-1=0,求代数式
(1)2x2+2x-4的值;
(2)x3+2x2-7的值.
(1)2x2+2x-4的值;
(2)x3+2x2-7的值.
考点:因式分解的应用
专题:
分析:由条件可求得x2+x=1,再整体代入即可.
解答:解:∵x2+x-1=0,
∴x2+x=1,
(1)2x2+2x-4=2(x2+x)-4=2×1-4=2-4=-2;
(2)x3+2x2-7=x3+x2+x2-7=x(x2+x)+x2-7=x+x2-7=x2+x-7=1-7=-6.
∴x2+x=1,
(1)2x2+2x-4=2(x2+x)-4=2×1-4=2-4=-2;
(2)x3+2x2-7=x3+x2+x2-7=x(x2+x)+x2-7=x+x2-7=x2+x-7=1-7=-6.
点评:本题主要考查整体思想求值,解题的关键是把x2+x看成一个整体代入求值.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
下列说法中正确的是( )
| A、两个平行四边形一定相似 |
| B、两个菱形一定相似 |
| C、两个矩形一定相似 |
| D、两个等腰直角三角形一定相似 |
下列说法正确的是( )
| A、无限小数都是无理数 |
| B、无理数都是无限小数 |
| C、有理数都是有限小数 |
| D、π+2是有理数 |
已知一元二次方程x2+3x+1=0,下列判断正确的是( )
| A、该方程有两个相等的实数根 |
| B、该方程有两个不相等的实数根 |
| C、该方程无实数根 |
| D、该方程根的情况不确定 |
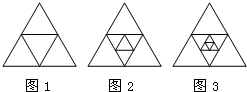 如图,在图1中,互不重叠的三角形共有4个,在图,2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,…,则在第9个图形中,互不重叠的三角形共有
如图,在图1中,互不重叠的三角形共有4个,在图,2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,…,则在第9个图形中,互不重叠的三角形共有 △ABC中,AB=61cm,BC=22cm,BC边上的中线AD=60cm,试说明△ABC是等腰三角形.
△ABC中,AB=61cm,BC=22cm,BC边上的中线AD=60cm,试说明△ABC是等腰三角形.