题目内容
某几何体的三视图如图所示，则组成该几何体共用了（ ）| A、12块小方块 |
| B、9块小方块 |
| C、7块小方块 |
| D、6块小方块 |
考点：由三视图判断几何体
专题：
分析：观察该几何体的三视图发现该几何体共有三层，第一层有三个，第二层有两个，第三层也有两个，由此可以得到答案．
解答：解：∵观察该几何体的三视图发现该几何体共有三层，第一层有三个，第二层有两个，第三层也有两个，
∴该几何体共有3+2+2=7块小方形，
故选C．
∴该几何体共有3+2+2=7块小方形，
故选C．
点评：本题考查了由三视图判断几何体的知识，解题的关键是会利用物体的三视图判断出该几何体的形状．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
若A（x1，y1），B（x2，y2），C（x3，y3）是反比例函数y=
图象上的点，且x1＜x2＜0＜x3，则y1、y2、y3的大小关系正确的是（ ）
| k2+1 |
| x |
| A、y3＞y1＞y2 |
| B、y1＞y2＞y3 |
| C、y2＞y1＞y3 |
| D、y3＞y2＞y1 |
为了检查一批零件的长度，从中取50个进行检测，在这个问题中个体是（ ）
| A、零件长度的全体 |
| B、50 |
| C、50个零件 |
| D、每个零件的长度 |
如图，直线DA切⊙O于A，AB是⊙O的一条直径，点C是⊙O上异于A、B的任一点，则下列结论不一定正确的是（ ）A、∠CAB=
| ||
| B、AD∥OC | ||
| C、AD2=DC•DB | ||
| D、AB⊥AD |
已知二次函数y=kx2-2x+1与一次函数y=k(x-1)-
的图象对于任意的非零实数k都有公共点，则k的取值范围是（ ）
| k |
| 4 |
| A、-1≤k≤1且k≠0 |
| B、-1≤k≤1 |
| C、k≤-1或k≥1 |
| D、任意实数 |
如图，为了绿化小区，某物业公司要在形如五边形ABCDE的草坪上建一个矩形花坛PKDH．已知：PH∥AE，PK∥BC，DE=100米，EA=60米，BC=70米，CD=80米．以BC所在直线为x轴，AE所在直线为y轴，建立平面直角坐标系，坐标原点为O．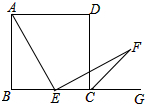
如图，在正方形ABCD中，边长AB=3，点E（与B，C不重合）是BC边上任意一点，把EA绕点E顺时针方向旋转90°到EF，连接CF．