题目内容
已知正比例函数y=kx的图象经过点（2，-4）、（1，y1）、（-1，y2），那么y1与y2的大小关系是（ ）
分析：利用待定系数法求得k=-2＜0，则该正比例函数经过第二、四象限，且y随x的增大而减小，据此可以比较y1与y2的大小．
解答：解：∵正比例函数y=kx的图象经过点（2，-4），
∴k=
=
=-2．则k＜0，
∴正比例函数y=-2x的图象经过第二、四象限，且y随x的增大而减小．
又∵1＞-1，
∴y1＜y2．
故选A．
∴k=
| y |
| x |
| -4 |
| 2 |
∴正比例函数y=-2x的图象经过第二、四象限，且y随x的增大而减小．
又∵1＞-1，
∴y1＜y2．
故选A．
点评：本题考查了一次函数图象上点的坐标特点．此题利用了正比例函数图象的性质来解答问题．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
已知正比例函数y=k1x（k1≠0）与反比例函数y=
（k2≠0）的图象有一个交点的坐标为（-2，-1），则它的另一个交点的坐标是（ ）
| k2 |
| x |
| A、（2，1） |
| B、（-2，-1） |
| C、（-2，1） |
| D、（2，-1） |
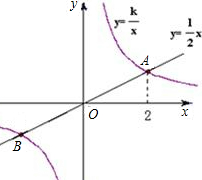横坐标为2．
如图，已知正比例函数和反比例函数的图象都经过点A（3，3）．