题目内容
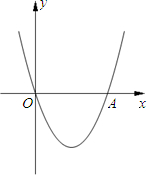 已知:如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.
已知:如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使锐角△AOB的面积等于3.求点B的坐标.
分析:(1)把(0,0)代入已知函数解析式即可求得k的值;
(2)利用面积法求得点B的纵坐标,然后由二次函数图象上点的坐标特征来求点B的横坐标即可.
(2)利用面积法求得点B的纵坐标,然后由二次函数图象上点的坐标特征来求点B的横坐标即可.
解答: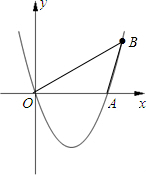 解:(1)如图,∵二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于原点0=O,
解:(1)如图,∵二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于原点0=O,
∴k+1=0,
解得,k=-1,
故该二次函数的解析式是:y=x2-3x.
(2)∵△AOB是锐角三角形,∴点B在第四象限.
设B(x,y)(x>1.5,y<0).
令x2-3x=0,即(x-3)x=0,
解得x=3或x=0,
则点A(3,0),故OA=3.
∵锐角△AOB的面积等于3.
∴
OA•|y|=3,即
×3|y|=3,
解得,y=-2.
又∵点B在二次函数图象上,
∴-2=x2-3x,
解得x=2或x=1(舍去).
故点B的坐标是(2,-2).
 解:(1)如图,∵二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于原点0=O,
解:(1)如图,∵二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于原点0=O,∴k+1=0,
解得,k=-1,
故该二次函数的解析式是:y=x2-3x.
(2)∵△AOB是锐角三角形,∴点B在第四象限.
设B(x,y)(x>1.5,y<0).
令x2-3x=0,即(x-3)x=0,
解得x=3或x=0,
则点A(3,0),故OA=3.
∵锐角△AOB的面积等于3.
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得,y=-2.
又∵点B在二次函数图象上,
∴-2=x2-3x,
解得x=2或x=1(舍去).
故点B的坐标是(2,-2).
点评:本题考查了二次函数的性质,解答(2)题时需要注意点B是位于这条抛物线的对称轴右边的图象上有一点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
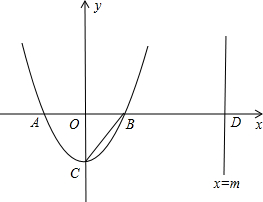 左边),与y轴交于点C.直线x=m(m>2)与x轴交于点D.
左边),与y轴交于点C.直线x=m(m>2)与x轴交于点D.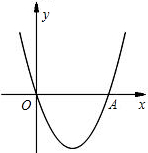 已知:如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.
已知:如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点. 已知,如图,二次函数y=ax2+2ax-3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l:
已知,如图,二次函数y=ax2+2ax-3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l: (2013•闸北区一模)已知:如图,二次函数
(2013•闸北区一模)已知:如图,二次函数 已知:如图,二次函数y=ax2-2ax+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
已知:如图,二次函数y=ax2-2ax+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).