题目内容
 如图,在一笔直的公路上有相距2000米的A、B两点,此时公路的正上方有一架飞机C,小明站在点A处,看飞机C,测得仰角为30°,小王在B处看飞机C,测得仰角为45°,求此时飞机的大约高度CD.(小明、小王的身高忽略不计,参考数据
如图,在一笔直的公路上有相距2000米的A、B两点,此时公路的正上方有一架飞机C,小明站在点A处,看飞机C,测得仰角为30°,小王在B处看飞机C,测得仰角为45°,求此时飞机的大约高度CD.(小明、小王的身高忽略不计,参考数据 ≈1.4,
≈1.4, ≈1.7,结果精确到1米)
≈1.7,结果精确到1米)
解:设CD=x米,
根据题意得:∠A=30°,∠B=45°,CD⊥AB,AB=2000米,
在Rt△ACD中,AD= =
= x(米),
x(米),
在Rt△BCD中,BD=CD=x(米),
∵AD+BD=AB,
∴ x+x=2000,
x+x=2000,
解得:x=1000 -1000≈700(米)
-1000≈700(米)
答:此时飞机的大约高度CD为700米.
分析:首先设CD=x米,根据题意得:∠A=30°,∠B=45°,CD⊥AB,AB=2000米,然后分别在Rt△ACD与Rt△BCD中,利用正切函数,即可表示出AD与BD的值,继而可得方程: x+x=2000,解此方程即可求得答案.
x+x=2000,解此方程即可求得答案.
点评:此题考查了仰角的定义.此题难度适中,注意能借助于解直角三角形的知识求解是解此题的关键,注意数形结合思想与方程思想的应用.
根据题意得:∠A=30°,∠B=45°,CD⊥AB,AB=2000米,
在Rt△ACD中,AD=
 =
= x(米),
x(米),在Rt△BCD中,BD=CD=x(米),
∵AD+BD=AB,
∴
 x+x=2000,
x+x=2000,解得:x=1000
 -1000≈700(米)
-1000≈700(米)答:此时飞机的大约高度CD为700米.
分析:首先设CD=x米,根据题意得:∠A=30°,∠B=45°,CD⊥AB,AB=2000米,然后分别在Rt△ACD与Rt△BCD中,利用正切函数,即可表示出AD与BD的值,继而可得方程:
 x+x=2000,解此方程即可求得答案.
x+x=2000,解此方程即可求得答案.点评:此题考查了仰角的定义.此题难度适中,注意能借助于解直角三角形的知识求解是解此题的关键,注意数形结合思想与方程思想的应用.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
 能否实现与指挥中心用对讲机通话.(参考数据:sin36°=0.59,cos36°=0.81,tan36°=0.73)
能否实现与指挥中心用对讲机通话.(参考数据:sin36°=0.59,cos36°=0.81,tan36°=0.73)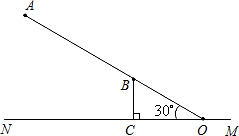 ,直线AB与公路MN的夹角∠AON=30°,新开发区B到公路MN的距离BC=3千米.
,直线AB与公路MN的夹角∠AON=30°,新开发区B到公路MN的距离BC=3千米.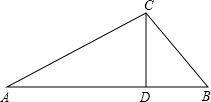 (2012•包河区二模)如图,在一笔直的公路上有相距2000米的A、B两点,此时公路的正上方有一架飞机C,小明站在点A处,看飞机C,测得仰角为30°,小王在B处看飞机C,测得仰角为45°,求此时飞机的大约高度CD.(小明、小王的身高忽略不计,参考数据
(2012•包河区二模)如图,在一笔直的公路上有相距2000米的A、B两点,此时公路的正上方有一架飞机C,小明站在点A处,看飞机C,测得仰角为30°,小王在B处看飞机C,测得仰角为45°,求此时飞机的大约高度CD.(小明、小王的身高忽略不计,参考数据 ≈1.4,
≈1.4, ≈1.7,结果精确到1米)
≈1.7,结果精确到1米)