题目内容
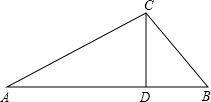 (2012•包河区二模)如图,在一笔直的公路上有相距2000米的A、B两点,此时公路的正上方有一架飞机C,小明站在点A处,看飞机C,测得仰角为30°,小王在B处看飞机C,测得仰角为45°,求此时飞机的大约高度CD.(小明、小王的身高忽略不计,参考数据
(2012•包河区二模)如图,在一笔直的公路上有相距2000米的A、B两点,此时公路的正上方有一架飞机C,小明站在点A处,看飞机C,测得仰角为30°,小王在B处看飞机C,测得仰角为45°,求此时飞机的大约高度CD.(小明、小王的身高忽略不计,参考数据| 2 |
| 3 |
分析:首先设CD=x米,根据题意得:∠A=30°,∠B=45°,CD⊥AB,AB=2000米,然后分别在Rt△ACD与Rt△BCD中,利用正切函数,即可表示出AD与BD的值,继而可得方程:
x+x=2000,解此方程即可求得答案.
| 3 |
解答:解:设CD=x米,
根据题意得:∠A=30°,∠B=45°,CD⊥AB,AB=2000米,
在Rt△ACD中,AD=
=
x(米),
在Rt△BCD中,BD=CD=x(米),
∵AD+BD=AB,
∴
x+x=2000,
解得:x=1000
-1000≈700(米)
答:此时飞机的大约高度CD为700米.
根据题意得:∠A=30°,∠B=45°,CD⊥AB,AB=2000米,
在Rt△ACD中,AD=
| CD |
| tan30° |
| 3 |
在Rt△BCD中,BD=CD=x(米),
∵AD+BD=AB,
∴
| 3 |
解得:x=1000
| 3 |
答:此时飞机的大约高度CD为700米.
点评:此题考查了仰角的定义.此题难度适中,注意能借助于解直角三角形的知识求解是解此题的关键,注意数形结合思想与方程思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
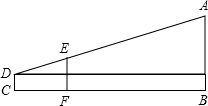 (2012•包河区二模)如图所示,在数学活动课上,几个同学用如下方法测量学校旗杆的高度:人站在距旗杆AB底部40米的C处望旗杆顶A,水平移动标杆EF,使C、F、B在同一直线上,D、E、A也在同一直线上,此时测得CF距离为2.5米,已知标杆EF长2.5米,人的视线高度CD为1.5米.则旗杆AB高为( )
(2012•包河区二模)如图所示,在数学活动课上,几个同学用如下方法测量学校旗杆的高度:人站在距旗杆AB底部40米的C处望旗杆顶A,水平移动标杆EF,使C、F、B在同一直线上,D、E、A也在同一直线上,此时测得CF距离为2.5米,已知标杆EF长2.5米,人的视线高度CD为1.5米.则旗杆AB高为( )