Question

如图所示，在一笔直的公路MN的同一旁有两个新开发区A，B，已知AB=10千米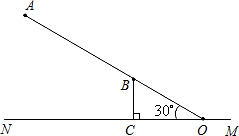，直线AB与公路MN的夹角∠AON=30°，新开发区B到公路MN的距离BC=3千米．
（1）新开发区A到公路MN的距离为

 

；
（2）现要在MN上某点P处向新开发区A，B修两条公路PA，PB，使点P到新开发区A，B的距离之和最短．此时PA+PB=

 

（千米）．

Answer 1

分析：（1）先求出OB的长，从而得出OA的长，再根据三角函数求得到公路的距离．
（2）根据切线的性质得EF=CD=BC=3，AF=AE+EF=AE+BC=11，再根据余弦概念求解．

解答：解：（1）∵BC=3，∠AOC=30°，
∴OB=6．
过点A作AE⊥MN于点E，AO=AB+OB=16，
∴AE=8．
即新开发区A到公路的距离为8千米；

（2）过D作DF⊥AE的延长线（点D是点B关于MN的对称点），垂足为F．
则EF=CD=BC=3，AF=AE+EF=AE+BC=11，
过B作BG⊥AE于G，
∴BG=DF，
∵BG=AB•cos30°=5

3

，
∴AD=

AF2+DF2

=

112+(5 3  )2

=

196

=14，
连接PB，则PB=PD，
∴PA+PB=PA+PD=AD=14（千米）．

点评：此题主要考查学生利用轴对称的性质来综合解三角形的能力．