题目内容
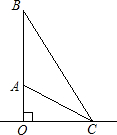
如图,大楼高30m,附近有一座塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶的仰角为30°,求塔高BC及大楼与塔之间的距离AC(结果精确到0.01m,参考数据:
≈1.732,
≈1.414)

| 3 |
| 2 |

设塔高BC为xm.
在Rt△ABC中,tan∠BAC=
,
∴AC=
=
=
,(2分)
在Rt△BDE中,tan∠BDE=
,
∴DE=
=
=
,(4分)
∵AC=DE,
∴
=
,(6分)
解,得x=45(m),(8分)
这时AC=
=
≈25.98(m),(10分)
答:塔高BC为45米,大楼与塔之间的距离AC约是25.98米.(11分)
在Rt△ABC中,tan∠BAC=
| BC |
| AC |
∴AC=
| BC |
| tan∠BAC |
| x |
| tan600 |
| x | ||
|
在Rt△BDE中,tan∠BDE=
| BE |
| DE |
∴DE=
| BE |
| tan∠BDE |
| x-30 |
| tan30° |
| 3(x-30) | ||
|
∵AC=DE,
∴
| x | ||
|
| 3(x-30) | ||
|
解,得x=45(m),(8分)
这时AC=
| x | ||
|
| 45 | ||
|
答:塔高BC为45米,大楼与塔之间的距离AC约是25.98米.(11分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



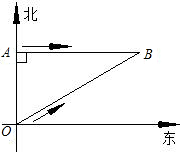 查,巡逻艇调整好航向,以26海里/小时的速度追赶,在涉嫌船只不改变航向和航速的前提下,问:
查,巡逻艇调整好航向,以26海里/小时的速度追赶,在涉嫌船只不改变航向和航速的前提下,问: