题目内容
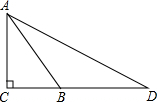
如图,在Rt△ABC中,∠C=90°,cos∠CAB=
,AC=8,延长CB到D使得BD=AB,连接AD,求AD的长.
| 4 |
| 5 |

∵在Rt△ABC中,∠C=90°,
∴cos∠CBA=
=
,
∵AC=8,
∴AB=10,
∴由勾股定理得:BC=
=6,
∴BD=AB=10,CD=BD+CB=16,
在Rt△ACD中,由勾股定理得:AD=
=8
.
∴cos∠CBA=
| AC |
| AB |
| 4 |
| 5 |
∵AC=8,
∴AB=10,
∴由勾股定理得:BC=
| 102-82 |
∴BD=AB=10,CD=BD+CB=16,
在Rt△ACD中,由勾股定理得:AD=
| 82+162 |
| 5 |

练习册系列答案
相关题目
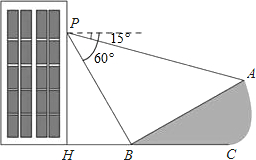
 向移动(如图所示).在离台风中心250千米的范围内将受台风影响.
向移动(如图所示).在离台风中心250千米的范围内将受台风影响.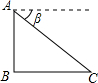


 适当的字母).
适当的字母).