题目内容
如图，在菱形ABCD中，对角线AC与BD相交于点O，OE∥DC，交BC于点E，AD=8，则OE的长为（ ）| A、8 | B、4 | C、3 | D、2 |
考点：菱形的性质
专题：
分析：根据已知可得OE是△ABC的中位线，从而求得OE的长．
解答：解：∵OE∥DC，AO=CO，
∴OE是△ABC的中位线，
∵四边形ABCD是菱形，
∴AB=AD=8，
∴OE=4．
故选B．
∴OE是△ABC的中位线，
∵四边形ABCD是菱形，
∴AB=AD=8，
∴OE=4．
故选B．
点评：本题考查了菱形的性质及三角形的中位线定理，属于基础题，关键是得出OE是△ABC的中位线，难度一般．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
某校开展“好书伴我成长”的读书活动，为了解八年级450名学生的读书情况，随机调查了八年级50名学生本学期读书的册数，并将统计数据制成了扇形统计图，则该校八年级读书册数等于3册的约有分式方程
=
的解为（ ）
| 1 |
| x-1 |
| 2 |
| x2-1 |
| A、1 | B、-1 | C、无解 | D、±1 |
在正比例函数y=kx中，y随着x的增大而减小，则直线y=kx-k一定不经过（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到AB的距离是（ ）| A、3 | B、4 | C、15 | D、7.2 |
平面直角坐标系中有A（-2，-1），B（-4，3），C（0，0），则三角形ABC的面积为（ ）
| A、5 | B、6 | C、8 | D、3 |
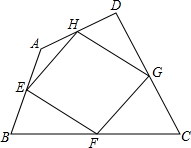如图，我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形．