题目内容
长方形的周长为14，一组邻边的长x、y满足（x-y）2-2（x-y）+1=0，则这个长方形的面积为（ ）
分析：所给方程可以整理为一个完全平方式子，可得x-y的值，根据长方形的周长可得x+y的值，进而求得x，y的值，相乘即为长方形的面积．
解答：解：设x＞y，
（x-y）2-2（x-y）+1=0，
（x-y）2=1，
∴x-y=±1，
x-y=1，
∵长方形的周长为14，
∴x+y=7，
∴x=4，y=3，
∴这个长方形的面积为12．
故选C．
（x-y）2-2（x-y）+1=0，
（x-y）2=1，
∴x-y=±1，
x-y=1，
∵长方形的周长为14，
∴x+y=7，
∴x=4，y=3，
∴这个长方形的面积为12．
故选C．
点评：综合考查了长方形的性质和完全平方公式，解二元一次方程组的方法；判断出x，y差的关系是解决本题的突破点．
练习册系列答案
小学课时特训系列答案
相关题目
，
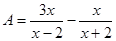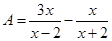，求A与B的积；
，
，求A与B的积；