题目内容
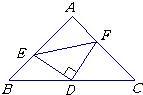10、如图，已知D为△ABC边BC的中点，DE⊥DF，则BE+CF（ ）分析：求证BE，CF，EF之间的关系，应利用全等，把它们整理到一个三角形中进行讨论．倍长中线法求解．
解答：
解：延长ED到G使DG=ED，连接CG，FG，
BD=CD，∠BDE=∠CDG，
可证得△BED≌△CGD，
∴CG=BE，
∵DE⊥DF，DG=ED，
∴EF=FG，
在△FCG中，FC+CG＞FG，
∴BE+CF＞EF．
故选A．
解：延长ED到G使DG=ED，连接CG，FG，BD=CD，∠BDE=∠CDG，
可证得△BED≌△CGD，
∴CG=BE，
∵DE⊥DF，DG=ED，
∴EF=FG，
在△FCG中，FC+CG＞FG，
∴BE+CF＞EF．
故选A．
点评：本题考查了全等三角形的判定及性质；出现中线问题暂时无法解决时，可延长过线成原来的2倍，利用SAS来构造全等三角形，这是一种很重要的解题方法，注意掌握．
练习册系列答案
名校课堂系列答案
相关题目
3、如图，已知⊙O，AB为直径，AB⊥CD，垂足为E，由图你还能知道哪些正确的结论请把它们一一写出来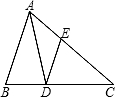
如图，已知AD为△ABC的角平分线，DE∥AB，如果
（2011•成华区二模）如图，已知半径为R的⊙O1的直径AB和弦CD交于点M，点A为
（2012•苏州）如图，已知半径为2的⊙O与直线l相切于点A，点P是直径AB左侧半圆上的动点，过点P作直线l的垂线，垂足为C，PC与⊙O交于点D，连接PA、PB，设PC的长为x（2＜x＜4）．