题目内容
18.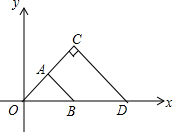 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为(1,1).
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为(1,1).
分析 首先利用等腰直角三角形的性质得出A点坐标,再利用位似是特殊的相似,若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k,△ABC上一点的坐标是(x,y),则在△A′B′C′中,它的对应点的坐标是(kx,ky)或(-kx,-ky),进而求出即可.
解答 解:∵∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,点B的坐标为(1,0),
∴BO=1,则AO=AB=$\frac{\sqrt{2}}{2}$,
∴A($\frac{1}{2}$,$\frac{1}{2}$),
∵等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,
∴点C的坐标为:(1,1).
故答案为:(1,1).
点评 此题主要考查了位似变换的性质,正确理解位似与相似的关系,记忆关于原点位似的两个图形对应点坐标之间的关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列变形属于移项的是( )
| A. | 由$\frac{x}{5}$=1,得x=5 | B. | 由-7x=2,得x=-$\frac{2}{7}$ | ||
| C. | 由-5x-2=0,得-2=5x | D. | 由-3+2x=9,得2x-3=9 |
8.$\sqrt{25}$表示的意义是( )
| A. | 25的立方根 | B. | 25的平方根 | C. | 25的算术平方根 | D. | 5的算术平方根 |
 如图,矩形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,线段EF与BH相交于点P,DF与GH相交于点Q.若四边形HPFQ是矩形,则$\frac{AB}{BC}$的值为$\frac{\sqrt{2}}{2}$.
如图,矩形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,线段EF与BH相交于点P,DF与GH相交于点Q.若四边形HPFQ是矩形,则$\frac{AB}{BC}$的值为$\frac{\sqrt{2}}{2}$.