题目内容
3.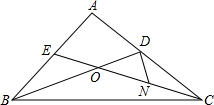 如图,在△ABC中,BD、CE是边AC、AB上的中线,BD与CE相交于点O,N是OC的中点.
如图,在△ABC中,BD、CE是边AC、AB上的中线,BD与CE相交于点O,N是OC的中点.(1)求证:OC=2OE;
(2)若S△CDN=1,求△ABC的面积.
分析 (1)根据重心的定义,由BD、CE是边AC、AB上的中线得到点O为△ABC的重心,然后根据重心的性质易得OC=2OE;
(2)根据三角形面积公式易得S△OCD=2S△CDN=2,再利用重心的性质得OB:OD=2:1,则S△BCD=3S△OCD=6,然后利用AD=CD可得S△ABC=2S△BCD=12.
解答 (1)证明:∵BD、CE是边AC、AB上的中线,
∴点O为△ABC的重心,
∴OC:OE=2:1,
即OC=2OE;
(2)解:∵N是OC的中点,
∴S△OCD=2S△CDN=2,
∵点O为△ABC的重心,
∴OB:OD=2:1,
∴S△BCD=3S△OCD=6,
∵BD为中线,
∴AD=CD,
∴S△ABC=2S△BCD=12.
点评 本题考查了三角形重心:三角形的重心是三角形三边中线的交点.重心到顶点的距离与重心到对边中点的距离之比为2:1.也考查了三角形面积公式.

练习册系列答案
相关题目
15.下列计算正确的是( )
| A. | 2a+3b=5ab | B. | (-1)0=1 | C. | (ab3)2=ab6 | D. | (x+2)2=x2+4 |
13.已知一组数据2,x,4,6的众数为4,则这组数据的平均数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
13.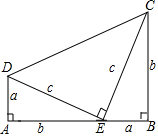 用两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图,通过用不同的方法计算这个图形的面积,可以得到哪一个等式( )
用两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图,通过用不同的方法计算这个图形的面积,可以得到哪一个等式( )
 用两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图,通过用不同的方法计算这个图形的面积,可以得到哪一个等式( )
用两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图,通过用不同的方法计算这个图形的面积,可以得到哪一个等式( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)(a+b)=a2-b2 | C. | a2+b2=c2 | D. | c2-a2=(c-a)(c+a) |
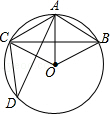 如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°,下列四个结论:
如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°,下列四个结论: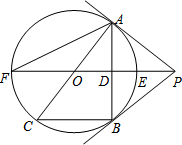 如图,PB为⊙O的切线,B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
如图,PB为⊙O的切线,B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF. 在平面直角坐标系中,已经A(8,0),B(0,6)
在平面直角坐标系中,已经A(8,0),B(0,6)