题目内容
19、如图，AB，CD是⊙O的两条直径，过点A作AE∥CD交⊙O于点E，连接BD，DE，求证：BD=DE．分析：连接OE，可得∠A=OEA，再由AE∥CD得∠BOD=∠A，∠DOE=∠OEA，从而得出∠BOD=∠DOE，则BD=DE．
解答：
证明：连接OE，如图，
∵OA=OE，∴∠A=∠OEA，
∵AE∥CD，∴∠BOD=∠A，∠DOE=∠OEA，
∴∠BOD=∠DOE，
∴BD=DE．
证明：连接OE，如图，∵OA=OE，∴∠A=∠OEA，
∵AE∥CD，∴∠BOD=∠A，∠DOE=∠OEA，
∴∠BOD=∠DOE，
∴BD=DE．
点评：此题主要考查了平行线的性质，在同圆中，等弦所对的圆心角相等．
练习册系列答案
相关题目
21、如图，AB、CD是⊙O的弦，∠A=∠C．求证：AB=CD．
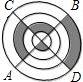如图，AB、CD是水平放置的轮盘（俯视图）上两条互相垂直的直径，一个小钢球在轮盘上自由滚动，该小钢球最终停在阴影区域的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
（2013•泰安）如图，AB，CD是⊙O的两条互相垂直的直径，点O1，O2，O3，O4分别是OA、OB、OC、OD的中点，若⊙O的半径为2，则阴影部分的面积为（ ）
（2013•盘锦）如图，AB，CD是⊙O的直径，点E在AB延长线上，FE⊥AB，BE=EF=2，FE的延长线交CD延长线于点G，DG=GE=3，连接FD．
如图，AB，CD是⊙O的两条弦，且AB=CD，点M是