题目内容
 已知△ABC为等边三角形,BD为中线,且BD=1,延长BC至E,使CE=CD,连接DE,求DE的长.
已知△ABC为等边三角形,BD为中线,且BD=1,延长BC至E,使CE=CD,连接DE,求DE的长.考点:等边三角形的性质,等腰三角形的性质
专题:
分析:先求出∠CBD=
ABC=30°,再求出∠E=30°,证出∠CBD=∠E,得出DE=BD=1.
| 1 |
| 2 |
解答:解:∵△ABC是等边三角形,
∴∠ACB=∠ABC=60°,
∵BD为中线,
∴∠CBD=
ABC=30°,
∵CE=CD,
∴∠E=∠CDE,
∵∠ACB=∠E+∠CDE,
∴∠E=30°,
∴∠CBD=∠E,
∴DE=BD=1.
∴∠ACB=∠ABC=60°,
∵BD为中线,
∴∠CBD=
| 1 |
| 2 |
∵CE=CD,
∴∠E=∠CDE,
∵∠ACB=∠E+∠CDE,
∴∠E=30°,
∴∠CBD=∠E,
∴DE=BD=1.
点评:本题考查了等边三角形的性质和等腰三角形的判定;熟练掌握等边三角形的性质和等腰三角形的判定是解决问题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图,化简|b-c|+|a+c|-|b-a|=
如图,化简|b-c|+|a+c|-|b-a|=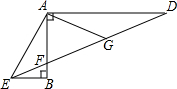 如图,∠ABE=∠BAD=90°,∠AED=2∠BED,点G是DF的中点,若BE=1,AG=4.
如图,∠ABE=∠BAD=90°,∠AED=2∠BED,点G是DF的中点,若BE=1,AG=4. 如图,小林根据在同一圆中圆心角、弧、弦三个量之间的关系认为,若∠AOB=2∠COD,则有
如图,小林根据在同一圆中圆心角、弧、弦三个量之间的关系认为,若∠AOB=2∠COD,则有
 如图,四边形OABC是矩形,且∠AOx=120°,CO=
如图,四边形OABC是矩形,且∠AOx=120°,CO= 如图,△ABC中,∠C=90°,AD是角平分线,AC=8,AD=
如图,△ABC中,∠C=90°,AD是角平分线,AC=8,AD=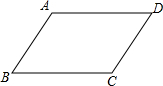 如图,已知?ABCD,求证:∠A=∠C,∠B=∠D(要求:不添加辅助线)
如图,已知?ABCD,求证:∠A=∠C,∠B=∠D(要求:不添加辅助线)